Оглавление.
1. Уравнение вида 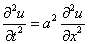 . Теоретическая часть.
. Теоретическая часть.
2. Пример №1 решения задачи на метод Фурье (свободные колебания струны).
3. Вынужденные колебания струны.
4. Пример решения задачи на нахождение вынужденных колебаний струны.
5. Пример (колебание струны с закрепленными концами в среде с сопротивлением).
В этой статье разобран метод Фурье или метод разделения переменных для уравнений гиперболического типа, рассматривая задачу о колебании струны. Теоретическая часть и задачи для примеров и решений взяты из «Сборник задач по уравнениям математической физики под ред. В.С. Владимирова».
Параграф 1. Самый простой случай.
Разберем простейшее уравнение, описывающее колебание струны, закрепленной на концах, без воздействия внешних сил.
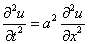 (1)
(1)
при начальных условиях
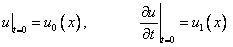 (2)
(2)
и граничных условиях
 . (3)
. (3)
Пояснение:
Начальное условие 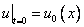 означает, что в нулевой момент времени струна имеет форму
означает, что в нулевой момент времени струна имеет форму 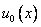 .
.
Начальное условие 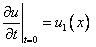 означает, что в нулевой момент времени скорости точек струны равны
означает, что в нулевой момент времени скорости точек струны равны 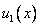 .
.
Граничные условия 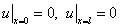 означают, что концы струны жестко закреплены.
означают, что концы струны жестко закреплены.
Метод Фурье, или метод разделения переменных основывается на том, что решение ищется в виде
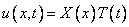 —
—
произведения двух функций, одна из которых зависит только от 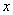 , а другая только от
, а другая только от 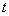 .
.
1) Найдем частные решения уравнения (1), не равные тождественно нулю и удовлетворяющие граничным условиям (3).
Подставим 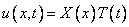 в исходное уравнение
в исходное уравнение 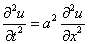 .
.
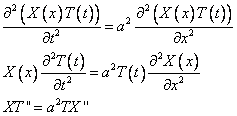
Поделим обе части полученного равенства на 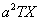
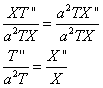
Пояснение: Получено равенство, левая часть которого зависит только от 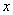 , а правая часть – только от
, а правая часть – только от 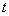 . Функции разных переменных могут быть равны между собой только в том случае, если они равны какому то числу, константе, обозначается эта константа
. Функции разных переменных могут быть равны между собой только в том случае, если они равны какому то числу, константе, обозначается эта константа 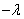 .
.
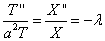
Получены два уравнения:
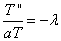 и
и 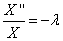 , или, после преобразований
, или, после преобразований
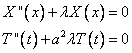
Рассмотрим первое из них. Необходимо найти нетривиальные (не равные тождественно нулю) решения этого уравнения, удовлетворяющие условиям
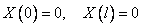 .
.
Замечание: Это есть граничные условия  .
.
Это задача Штурма-Лиувилля. Однако её может решить любой, изучивший курс дифференциальных уравнений.
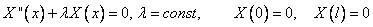 (4)
(4)
— линейное уравнение с постоянными коэффициентами. Составляем характеристическое уравнение:
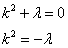
Замечание: Не вдаваясь в подробности: 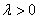 .
.
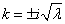
Общее решение уравнения (4):
 .
.
Определим значение коэффициентов 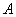 и
и 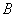 из условий
из условий 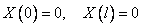 .
.
1) 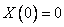
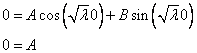
Подставляем в общее решение и получаем: 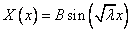 .
.
2) 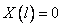
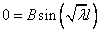
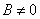 , иначе решением будет только
, иначе решением будет только 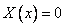 .
.
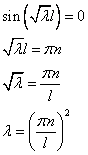
— это, в зависимости от  — собственные значения задачи.
— собственные значения задачи.
Т.к. выполнение условий не зависит от коэффициента 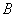 , то примем его значение равным 1.
, то примем его значение равным 1.
Итак, нетривиальными решениями уравнения (4) являются функции
 .
.
Решим уравнение 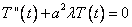 , причем уже известно, что
, причем уже известно, что  .
.
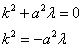
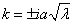
Общее решение уравнения (4):
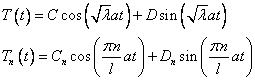 .
.
Возвращаемся к поставленной задаче (1):
Функции
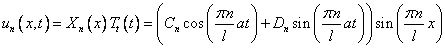
Являются частными решениями уравнения (1), удовлетворяющими условиям (3) .
Т.к. уравнение (1) линейно и однородно, то сумма частных решений
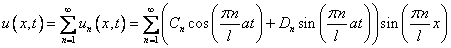
также является решением.
Теперь стоит разобраться с начальными условиями : 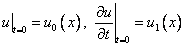 .
.
1) 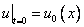
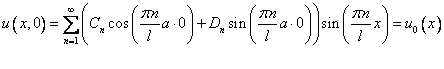
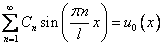 (5)
(5)
2) 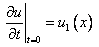
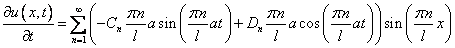
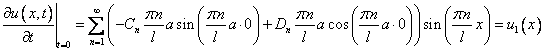
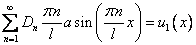 (6)
(6)
Замечание: Из теории рядов Фурье известно, что произвольная, кусочно-непрерывная и кусочно-дифференцируемая функция 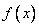 , заданная в промежутке
, заданная в промежутке 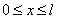 , разлагается в ряд Фурье
, разлагается в ряд Фурье
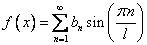 , где
, где 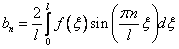 .
.
Можно заметить, что (5) и (6) есть разложения в ряд Фурье функций 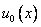 и
и 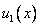 , а
, а 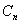 и
и 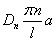 — коэффициенты этих разложений, значит, их можно определить по формулам
— коэффициенты этих разложений, значит, их можно определить по формулам
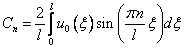 и
и  (7).
(7).
Вывод:
Ряд 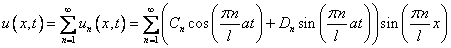
с коэффициентами
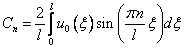 и
и 
является решением задачи (1) – (3).


