Задача о нахождении вынужденных колебаний однородной струны  , жестко закрепленной на концах, под действием внешней силы с плотностью
, жестко закрепленной на концах, под действием внешней силы с плотностью 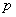 приводится к решению уравнения.
приводится к решению уравнения.
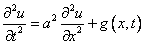 (8)
(8)
при начальных условиях
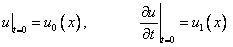 (9)
(9)
и граничных условиях
 . (10)
. (10)
Пояснение: 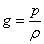 , где
, где 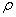 — линейная плотность струны.
— линейная плотность струны.
Решение этой задачи ищется в виде суммы
 ,
,
где:
1)  — решение неоднородного уравнения
— решение неоднородного уравнения 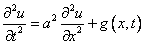 с граничными условиями
с граничными условиями 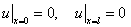 и начальными условиями
и начальными условиями 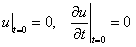 (решение неоднородного уравнения с нулевыми начальными и граничными условиями).
(решение неоднородного уравнения с нулевыми начальными и граничными условиями).
2)  — решение однородного уравнения
— решение однородного уравнения 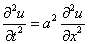 с граничными условиями
с граничными условиями 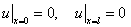 и начальными условиями
и начальными условиями 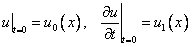 (решение однородного уравнения с условиями (9), (10)).
(решение однородного уравнения с условиями (9), (10)).
Пояснение: Как легко запомнить про  и
и  ? Очень просто: поставленная задача (8)-(10) имеет две «сложности»: неоднородность в виде слагаемого
? Очень просто: поставленная задача (8)-(10) имеет две «сложности»: неоднородность в виде слагаемого 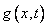 и ненулевые (в общем случае) начальные условия
и ненулевые (в общем случае) начальные условия 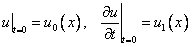 . Одну из этих сложностей обрабатываем в
. Одну из этих сложностей обрабатываем в  , а другую – в
, а другую – в  .
.
1. Найдем  . Для этого необходимо решить уравнение
. Для этого необходимо решить уравнение
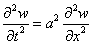
с граничными условиями

и начальными условиями
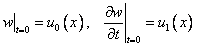 .
.
Формулировка задачи полностью совпадает с уравнением гиперболического типа, решенным методом Фурье в первом параграфе этой статьи. Решением является функция:
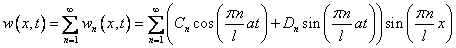
с коэффициентами
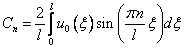 и
и 
Следует так же заметить, что при решении задачи были найдены собственные значения  и собственные функции
и собственные функции  .
.
2. Найдем  . Для этого нужно решить неоднородное уравнение
. Для этого нужно решить неоднородное уравнение
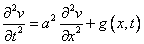
с граничными условиями

и начальными условиями
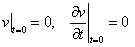 .
.
Решение ищется в виде:  . (11)
. (11)
Замечание: Используются собственные значения и собственные функции предыдущего уравнения.
Подставляем (11) в исходное уравнение (8).
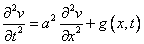
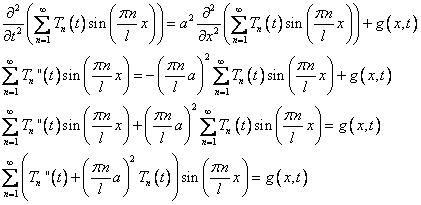
Разложим функцию 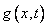 в ряд Фурье по синусам в интервале
в ряд Фурье по синусам в интервале  :
:
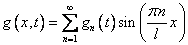
Сравниваем два последних равенства :

Отсюда можно составить дифференциальное уравнение:
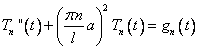 , где
, где 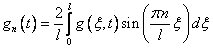 . (12)
. (12)
Причем решать это уравнение нужно при нулевых начальных условиях
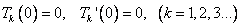 .
.
В задачнике В.С. Владимирова сказано (и это правда), что решение этого уравнения при таких начальных условиях можно записать в виде:
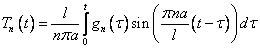 .
.
Замечание: Подробно получение этой формулы не рассматривается, т.к. если при решении конкретной задачи получилось уравнение вида (12), то следует просто применить эту формулу, а если получилось уравнение другого вида, то каждый конкретный случай нужно решать индивидуально.
Подставим это в (11) и получим выражение для  .
.
Итог:
Решение исходной задачи (8)-(10) представляется в виде:
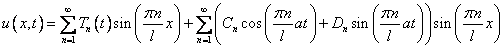 , где
, где
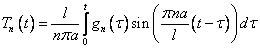 ,
,
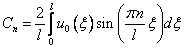 и
и 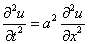 120.
120.


