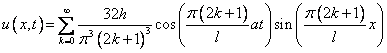Пример:
Решить задачу о колебании струны 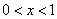с закрепленными концами, если начальные скорости точек равны нулю, внешние силы отсутствуют, а начальное отклонение 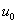имеет форму параболы, осью симметрии которой служит прямая 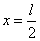, а вершиной – точка .
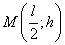Решение:
Составим уравнение, описывающее колебание этой струны:

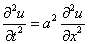
В данном случае:
а) т.к. концы закреплены, то .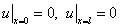
б) начальные скорости точек раны нулю: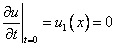
в) начальное отклонение 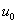имеет форму параболы, осью симметрии которой служит прямая 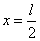, а вершиной – точка 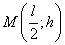. Составим уравнение этой параболы.
Общий вид уравнения параболы: 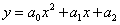. Известно, что эта парабола проходит через три точки: 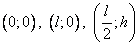, причем 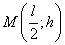— её вершина.
Подставим эти координаты в уравнение параболы и получим систему:

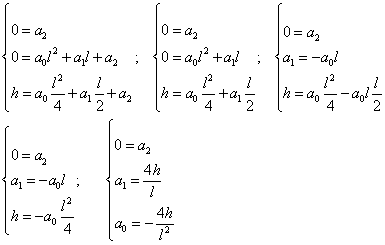
Итак, парабола задана уравнением:

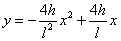
Задача составлена:


.
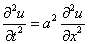
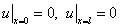
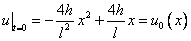Решим его методом разделения переменных.
Представим функцию 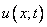как произведение двух функций, одна из которых завист только от 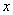, а другая только от :
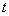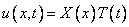
Уравнение и его граничные условия в точности соответствуют разобранному материалу в теоретической части, поэтому сразу можно записать решение:

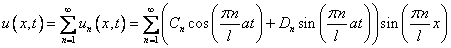
с коэффициентами
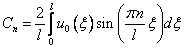и
Подставим значения 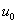и .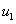

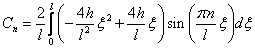
Для того, чтобы вычислить этот интеграл нужно дважды воспользоваться формулой интегрирования по частям.

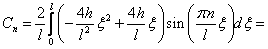
+ Показать/спрятать вычисления.

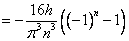
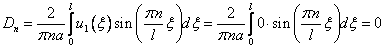
Поставляем вычисленные коэффициенты:

Замечание: Последнее преобразование объясняется тем, что при четном сомножитель 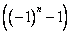равен 0, а при нечетном, т.е. , он равен -2.
Ответ: