Решить методом разделения переменных смешанную задачу:
 , (
, ( ),
), 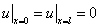 ,
,  .
.
Решение:
Решение этой задачи ищется в виде суммы
 ,
,
где:
1)  — решение неоднородного уравнения
— решение неоднородного уравнения  с граничными условиями
с граничными условиями 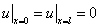 и начальными условиями
и начальными условиями  .
.
2)  — решение однородного уравнения
— решение однородного уравнения 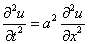 с граничными условиями
с граничными условиями  и начальными условиями
и начальными условиями  .
.
1. Найдем  . Для этого необходимо решить уравнение
. Для этого необходимо решить уравнение

с граничными условиями

и начальными условиями  .
.
Формулировка задачи полностью совпадает с уравнением гиперболического типа, решенным методом Фурье в первом параграфе этой статьи при 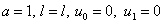 . Решением является функция:
. Решением является функция:

с коэффициентами
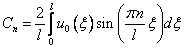 и
и 
Подставляем известные значения:

с коэффициентами
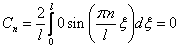 и
и 
Собственные значения

и собственные функции
 .
.
Получилось, что все коэффициенты равны 0, следовательно,
 .
.
2. Найдем  .
.
Решим уравнения  с граничными условиями
с граничными условиями  и начальными условиями
и начальными условиями 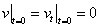 .
.
Решение ищется в виде:  .
.
Подставляем в исходное уравнение.


По общему методу необходимо разложим константу  в ряд Фурье по синусам в интервале
в ряд Фурье по синусам в интервале  :
:
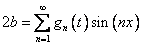

Подставляем это разложение в уравнение:
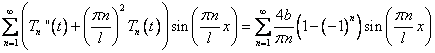
Отсюда можно составить дифференциальное уравнение:
 .
.
Причем решать это уравнение нужно при нулевых начальных условиях
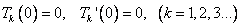 .
.
Решать его вручную нет необходимости, потому что в теоретической части указана формула для нахождения решений подобных уравнений:
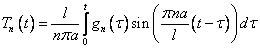

Замечание: Подробно получение этой формулы не рассматривается, т.к. если при решении конкретной задачи получилось уравнение вида (12), то следует просто применить эту формулу, а если получилось уравнение другого вида, то каждый конкретный случай нужно решать индивидуально.
Получим выражение для  .
.

Замечание: При четном  множитель
множитель  обращается в ноль. Т.к. вычисляются решения, не равные тождественно нулю, то в ответ запишем лишь ненулевые слагаемые, т.е. при
обращается в ноль. Т.к. вычисляются решения, не равные тождественно нулю, то в ответ запишем лишь ненулевые слагаемые, т.е. при  (нечетном).
(нечетном).

Ответ:
Решение исходной задачи :
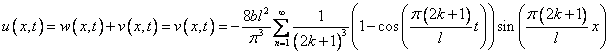 .
.
Замечание: Условие этой задачи взято из задачника Владимирова ( № 20.6 а) ), однако там дан ответ, отличный от приведенного здесь. Это можно объяснить либо какими-то преобразованиями полученного выражения ( хотя у меня не получилось привести виду в задачнике), либо опечаткой в условии. Правильность этого решения доказывает замечательная книга «Уравнения математической физики» под авторством И.Г. Арамановича и В.И. Левина, где в примере разобрана задача, аналогичная данной с точностью до константы.


