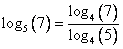0) Основное логарифмическое тождество:
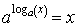 .
.1) Сумма логарифмом равна логарифму произведения:
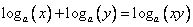
Замечание: для того, чтобы все слагаемые были определены, необходимо выполнение условии:
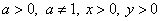 .
.Доказательство:
Из определения логарифма и свойств показательной функции следует, что
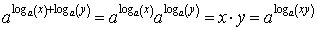
Т.к. из равенства
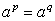 следует равенство
следует равенство 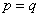 , то из равенства
, то из равенства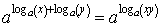
следует равенство
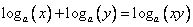
Свойство доказано.
Замечание: обратное свойство требует ограничений:
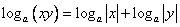
, т.к. произведение двух отрицательных чисел положительно, а логарифм от отрицательной величины неопределен.
Пример:
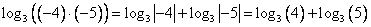
2) Логарифм степени:
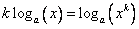
Доказательство:
Замечание: Т.к. выражение в левой части равенства определено, то
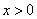 , а значит и
, а значит и 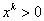 , т.е. определена и правая часть равенства.
, т.е. определена и правая часть равенства.
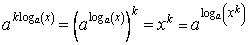
Т.к. из равенства
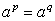 следует равенство
следует равенство 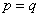 , то из равенства
, то из равенства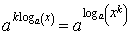
следует равенство
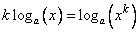 .
.Свойство доказано.
Пример:
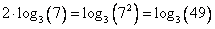
3) Разность логарифмом равна логарифму частного:
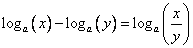
Замечание: для того, чтобы все слагаемые были определены, необходимо выполнение условии:
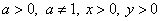 .
.Доказательство:
Можно доказывать это свойство тем же методом, что и предыдущие два, но можно и использовать комбинацию двух уже доказанных свойств.

Свойство доказано.
Замечание: обратное свойство требует ограничений:
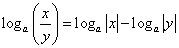 , т.к. частное двух отрицательных чисел положительно, а логарифм от отрицательной величины неопределен.
, т.к. частное двух отрицательных чисел положительно, а логарифм от отрицательной величины неопределен.Пример:
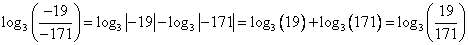
4) Формула перехода к новому основанию:
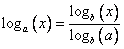
Доказательство:
Замечание: Т.к. выражение в левой части равенства определено, то
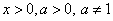 , значит, числитель и знаменатель правой части будут определены при любом
, значит, числитель и знаменатель правой части будут определены при любом 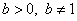 .
.Знаменатель этой дроби не равен нулю, т.к. логарифм равен нулю только в том, случае, если его аргумент равен 1 (
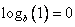 ) и известно, что
) и известно, что 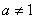 .
.
Доказывать равенство следует в виде:
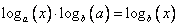
Из определения логарифма и свойств показательной функции следует, что
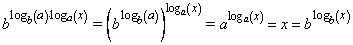
Т.к. из равенства
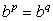 следует равенство
следует равенство 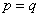 , то из равенства
, то из равенства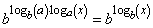
следует равенство 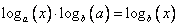 .
.
Свойство доказано.
Пример: