Пример 2.
Решить неравенство: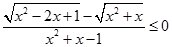 
Решение:
Проанализируем неравенство. Дробь сравнивается с нулем. Знаем, что дробь меньше нуля тогда и только тогда, когда числитель и знаменатель разных знаков. Дробь равна нулю тогда и только тогда, когда числитель равен нулю, а знаменатель не равен нулю. Т.о. получаем два случая:
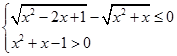или 
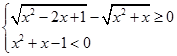.Целых две системы, в каждой из которых присутствует иррациональное неравенство. Слишком сложно.
Давайте применим метод рационализации.
Известно, что функция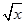 
— монотонно возрастающая, значит, выражения 
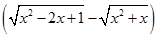и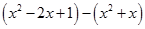 
имеют одинаковый знак и из исходного неравенства следует следующая система ( т.к. мы обязаны не забывать про неотрицательность подкоренных выражений:
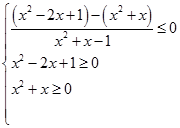
Решим второе неравенство:
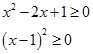
Квадрат чего-то всегда неотрицателен, значит х – любое.
Решим третье неравенство:
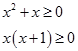
Метод интервалов:
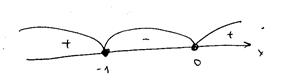
Решение третьего неравенства :
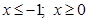
Решим первое неравенство:
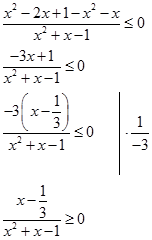
Разложим квадратный трехчлен в знаменателе на сомножители:
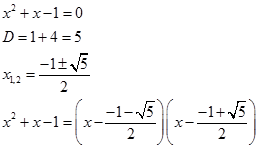
Подставим в неравенство:
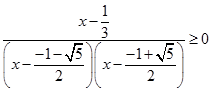
Применим метод интервалов:
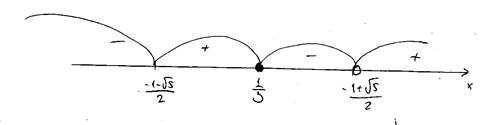
Решение первого неравенства:
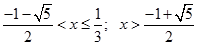
Запишем ответы в системе:
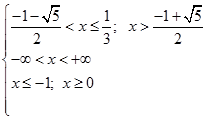
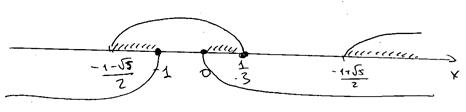
Ответ:
