Пример 3. Важный!
Решить неравенство: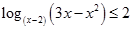 
Решение:
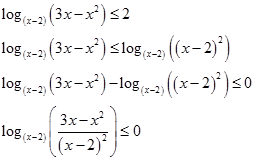
Дальнейшие размышления тормозятся отсутствием знания о возрастании или убывании этого логарифма, т.к. неизвестно, является ли основание логарифма большим или меньшим 1. Да и метод рационализации надо как то применить.
Перейдем к десятичным логарифмам по формуле перехода к новому основанию:
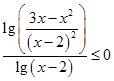
Теперь надо получить разность одинаковых функций в числителе и знаменателе.
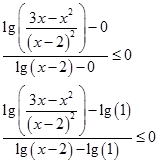
Знаем, что функция y=lg(x) — монотонно возрастающая, тогда, следуя методу рационализации, следствием этого неравенства является следующее:
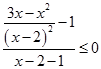
И, с учетом ОДЗ, получим систему:
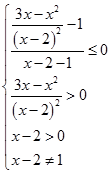
Решим первое неравенство системы
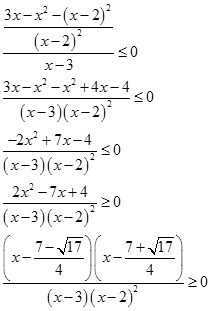
Применим метод интервалов:
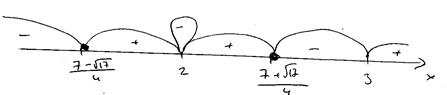
Ответ для этого неравенства:
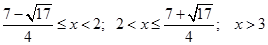
Теперь разберемся с ОДЗ:
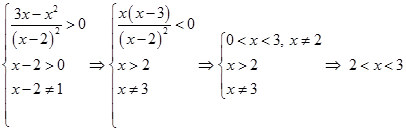
Пересечем с ответом:
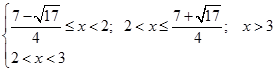
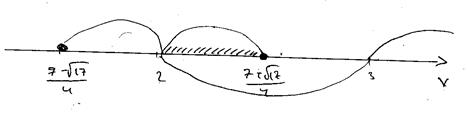
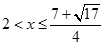
Ответ: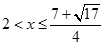
Важное замечание: Для решений неравенств типа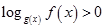 
( наиболее часто попадающихся в заданиях) не обязательно применять последовательно все шаги метода рационализации с получением дроби, с разностью одинаковых монотонных функций и т.д., следует запомнить лишь вот это:
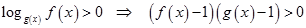.И не забыть про область определения функций!!!