Оглавление.
1. Монотонность и метод рационализации. Начало теории.
2. Пример применения метода рационализации.
3. Пример решения логарифмического неравенства методом рационализации. Важный!
4. Пример применения метода рационализации. Сложный!
Метод рационализации – правило, по которому можно свести неравенство, содержащее «противные» функции типа логарифмов или радикалов, синусов-косинусов и т.д. к рациональному неравенству, которое уже любой школьник сможет решить методом интервалов.
Вся соль метода рационализации заключается в понятии монотонной функции.
Определение: Функция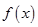 
называется монотонно возрастающей (убывающей), если для любых 
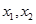из области определения таких, что 
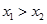, справедливо неравенство 
.
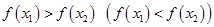Поясним определение графически:
| Монотонно возрастающая функция | Монотонно убывающая функция |
 |
 |
 |
 |
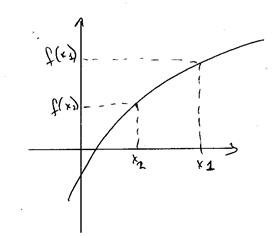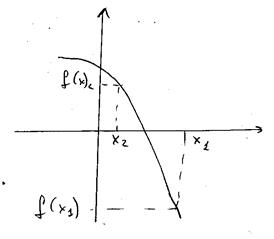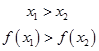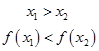Замечание: функция называется монотонной, если она монотонно возрастает или монотонно убывает.
Перейдем к описанию и применению самого метода рационализации.
Пусть функция 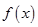монотонно возрастающая и числа 
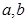принадлежат её области определения. Тогда, по определению монотонно возрастающей функции, из неравенства 
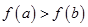следует неравенство 
.
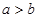Как следствие, утверждаем, что если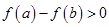 
, то 
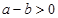, т.е. осознаем, что выражения 
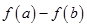и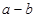 
имеют одинаковый знак.
Пример 1.
Решить неравенство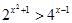 
Решение:
Преобразуем неравенство так, чтобы в его левой и правых частях стояли одинаковые функции.
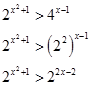
Т.е. функция
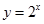возрастающая, то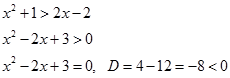
Квадратный трехчлен корней не имеет, т.е. парабола
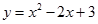оси абсцисс не пересекает, т.е. лежит выше неё и при любом значении х верно 
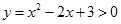.Ответ: х – любое.
Но для таких простых задач не стоило бы придумывать отдельный метод и называть его «метод рационализации». Усложним.
Пусть функции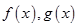 
— монотонно возрастающие.
Требуется решить неравенство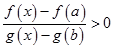 
.
Помним, что выражения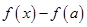 
и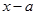 
имеют одинаковый знак. Аналогично для выражени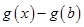й 
и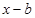 
.
Получим рациональное неравенство:
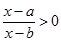.Его, конечно же, можно решить методом интервалов.
Заметим, что множество решений второго неравенства больше или равно множества решений исходного неравенства, т.к. следует не забывать об области определения функци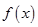й и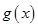 
.