Теоретическая подоплека:
1) Произведение двух сомножителей больше нуля тогда и только тогда, когда эти сомножители одного знака: либо оба положительны, либо оба отрицательны.
2) Произведение двух сомножителей меньше нуля тогда и только тогда, когда эти сомножители противоположных знаков: один из них положителен, а другой — отрицателен.
3) Произведение двух сомножителей равно нулю тогда и только тогда, когда хотя бы один из сомножителей равен нулю.
Эти утверждения легко проверить на обычных числах.
Замечание: в статье «решение квадратных неравенств» доказывалась формула разложения квадратного трехчлена на сомножители:
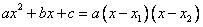 , где,
, где, 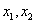 — корни квадратного трехчлена.
— корни квадратного трехчлена.
Пример 1: Решить неравенство: 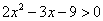 .
.
Разложим квадратный трехчлен 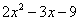 на сомножители (вдруг получится).
на сомножители (вдруг получится).

Неравенство примет вид:
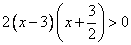
Разделим обе части неравенства на 2, т.е. на положительное число, а значит, знак неравенства не поменяется.
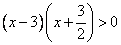
Произведение двух сомножителей больше нуля тогда и только тогда, когда эти сомножители одного знака: либо оба положительны, либо оба отрицательны.
1) Оба положительны.
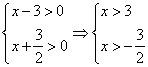
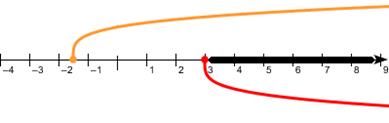
Ответ случая: 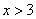
2) Оба отрицательны.
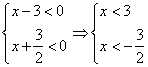
Ответ случая: 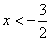
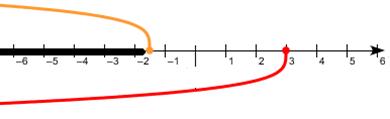
Объединим результаты случаев:
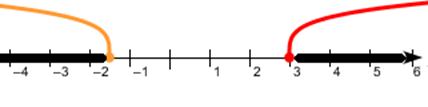
Объединение этих решений: 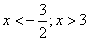
Ответ: 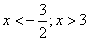
Пример 2: Решить неравенство: 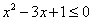 .
.
Разложим квадратный трехчлен 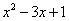 на сомножители (вдруг получится).
на сомножители (вдруг получится).

Неравенство примет вид:
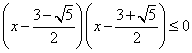
Произведение двух сомножителей меньше нуля тогда и только тогда, когда эти сомножители противоположных знаков: один из них положителен, а другой — отрицателен.
Произведение двух сомножителей равно нулю тогда и только тогда, когда хотя бы один из сомножителей равен нулю.
1) Первый сомножитель неотрицателен (больше или равен нулю), второй сомножитель неположителен (меньше или равен нулю).
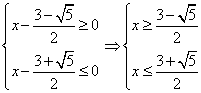
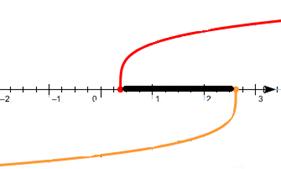
Ответ случая: 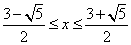
2) Первый сомножитель неположителен, второй сомножитель неотрицателен.
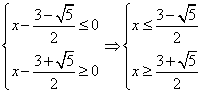
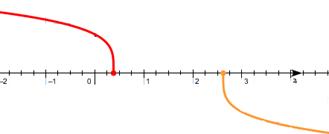
Решения первого и второго неравенства системы не пересекаются, значит, решений нет.
Ответ случая: решений нет.
Т.к. во втором случае нет решения, то решением всего неравенства будет ответ первого случая:
Ответ: 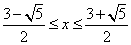 .
.
Пример 3. Решить неравенство 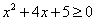
Разложим квадратный трехчлен 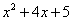 на сомножители (ну вот вдруг опять получится).
на сомножители (ну вот вдруг опять получится).
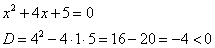
Корней нет. Квадратный трехчлен 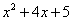 нельзя разложить на множители (над полем действительных чисел).
нельзя разложить на множители (над полем действительных чисел).
Не получилось.
Вывод: в таком случае лучше воспользоваться геометрическим методом, изложенным выше.


