Решение квадратных неравенств.
Квадратным будем называть неравенства вида:
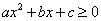или , .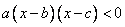
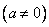Замечание: знак неравенства может быть любой, основным признаком того, что неравенство квадратное является то, что с нулем сравнивается многочлен второй степени.

В этой статье будут разобраны несколько методов решения квадратных неравенств и показана связь между этими методами.

Метод I .Основной, графический.

Пример 1: Решить неравенство 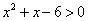. В левой части которого стоит квадратный трехчлен. Построим его график, т.е. график функции 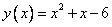. Всем известно, что графиком квадратичной функции является парабола.
Замечание: Алгоритм схематического построения параболы :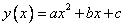
1) Выяснить направление ветвей.
Если 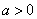, то ветви направлены вверх, если 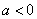, то вниз.
В случае 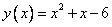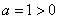— ветви направлены вверх.
2) Выяснить координаты пересечения графика с осью ОХ. Ординаты этих точек равны 0, т.е. в функцию 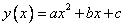необходимо подставить 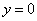и решить полученное уравнение .
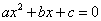В случае :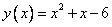

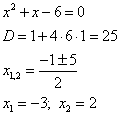
Таким образом, график функции 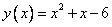пересекает ось ОХ в точках с координатами .

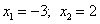Замечание: Если квадратное уравнение 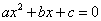не имеет корней, то парабола 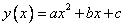ось абсцисс не пересекает.

3) Пункт необязателен в случае, если график параболы пересекает ось абсцисс.
Определить координаты вершин параболы : .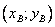
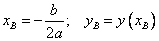В случае :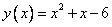

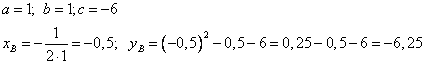
Координаты вершины: .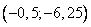
Построим параболу, опираясь на полученные факты:

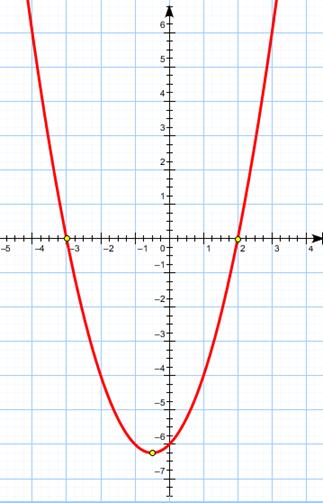
Напомним, что решается задача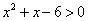
Исходное неравенство можно записать в ви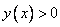де: , где .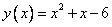
Решением будут абсциссы (координаты 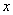) точек графика, ординаты (координаты 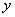) которых больше нуля, т.е. лежат в верхней полуплоскости. Поясним это утверждение на примере.
Пример (частный случай):
Рассмотрим точку А (см. рис.) с координатой .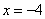

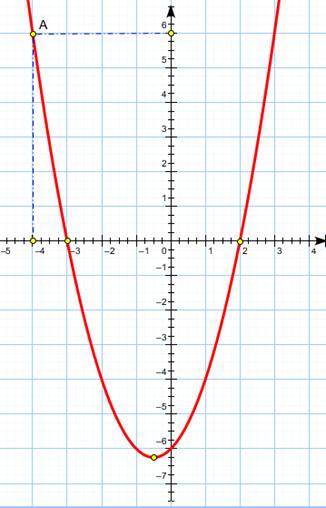
Она лежит в верхней полуплоскости, т.е. её абсцисса 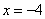является решением неравенства .
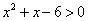Проверим это:
а) С алгебраической точки зрения:
Подставим 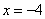в неравенство :

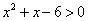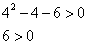
Неравенство верно, значит 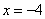является решением неравенства.
б) С геометрической точки зрения. Помним, что построена парабола 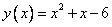и рассматривается точка А с абсциссой 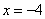. Вычислим ординату : 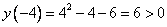. Ордината этой точки положительна, что невооруженным глазом видно на графике. т.е. неравенство 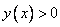выполняется.

Отметим синим цветом на чертеже участки графика, для которых выполняется условие :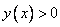

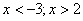
Запишем абсциссы этих точек (необходимые участки оси абсцисс обозначены штриховкой): 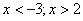. Это и будет ответом неравенства.
Ответ: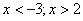

Пример 2:
Решить неравенство .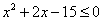
Построим схематично параболу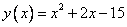
1) Направление ветвей.
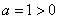, ветви параболы направлены вверх.
2) Пересечение с ОХ.

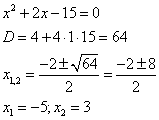
Парабола пересекает ось абсцисс в точках с координатами .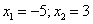
3) координаты вершины:

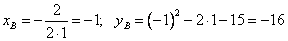
Координаты вершины параболы: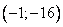
Построим график:

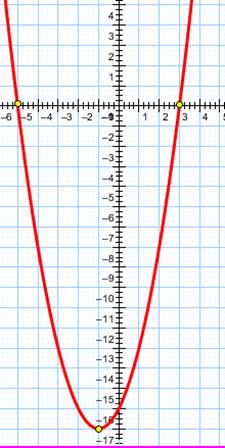
Неравенство 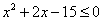можно записать ви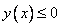де , где 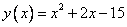. Т.е. для решения неравенства интересны точки, ординаты которых меньше или равны нулю, т.е. точки, лежащие в нижней полуплоскости или на оси ОХ.
Отметим эти точки:

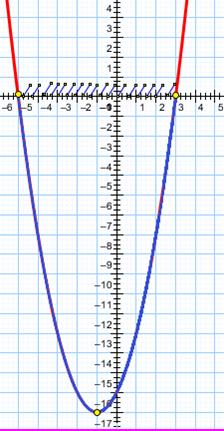
Штриховкой обозначим абсциссы этих точек и запишем это множество: 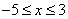. Эти значения переменной и будут решением неравенства.
Ответ: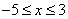

Пример 3:
Решить неравенство .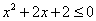
Построим схематично параболу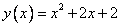
1) Направление ветвей.
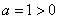, ветви параболы направлены вверх.
2) Пересечение с ОХ.

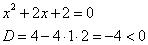
Корней нет.
Парабола не пересекает ось абсцисс.
3) Координаты вершины:

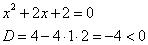
Координаты вершины параболы: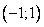
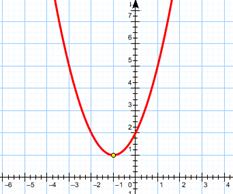
Построим график:

Неравенство 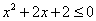можно записать ви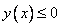де , где 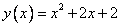. Т.е. для решения неравенства интересны точки, ординаты которых меньше или равны нулю, т.е. очки, лежащие в нижней полуплоскости или на оси ОХ. Таких точек нет, т.к. вся парабола лежит выше оси ОХ. Делаем соответствующий вывод.
Ответ: решений нет, т.е. не существует таких значений переменной 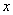, при которых неравенство 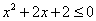— верное.