Вот и подошли мы к методу интервалов. Рассмотрим его урезанную версию – для решения квадратных неравенств.
Суть метода интервалов будет пояснена на примерах:
Пример 1. Решить неравенство: 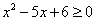 .
.
Разложим квадратный трехчлен на сомножители.
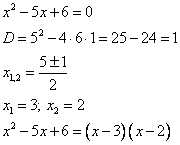
Неравенство примет вид:
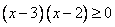
Выше обсуждалось, что знак произведения двух сомножителей (а произведение сравнивается с нулем, т.е. важны те значения переменной, при которых произведение 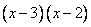 принимает неотрицательные значения) зависит только от знака каждого из сомножителей, и не зависит от их абсолютной величины.
принимает неотрицательные значения) зависит только от знака каждого из сомножителей, и не зависит от их абсолютной величины.
Грубо говоря, нам все равно: 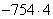 или
или 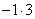 , потому что оба этих произведения отрицательны.
, потому что оба этих произведения отрицательны.
Итак, есть два сомножителя:
Первый : 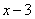 . Этот сомножитель меняет свой знак при
. Этот сомножитель меняет свой знак при 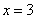 , т.е при
, т.е при 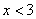 это выражение отрицательно:
это выражение отрицательно: 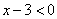 , а при
, а при 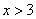 оно принимает положительные значения:
оно принимает положительные значения: 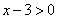 .
.
Второй: 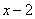 . Для этого сомножителя такая «знаковая» точка:
. Для этого сомножителя такая «знаковая» точка: 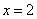 .
.
Вывод: знак произведения 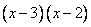 меняется только при переходе переменной через значения
меняется только при переходе переменной через значения 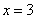 и
и 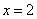 .
.
В этом и заключается смысл метода интервалов: определить интервалы значений переменной, на которых ситуация не меняется и рассматривать их как единое целое.
Построим чертеж.

Рассмотрим эти интервалы в том же порядке, как пишем и читаем: слева направо.
1) 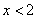 . На этом интервале ситуация не изменяется, значит, для того, чтобы определить ситуацию, можно взять любое значение из этого интервала и подставить его в произведение.
. На этом интервале ситуация не изменяется, значит, для того, чтобы определить ситуацию, можно взять любое значение из этого интервала и подставить его в произведение.
Например: 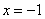
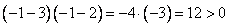
Вывод: при 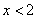 верно неравенство
верно неравенство 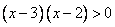
Внесем эти данные в чертеж. Это делать обязательно для визуализации процесса.

2) 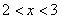 . На этом интервале ситуация не изменяется, значит, для того, чтобы определить ситуацию. Можно взять любое значение из этого интервала и подставить его в произведение.
. На этом интервале ситуация не изменяется, значит, для того, чтобы определить ситуацию. Можно взять любое значение из этого интервала и подставить его в произведение.
Например: 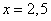
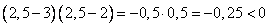
Вывод: при 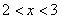 верно неравенство
верно неравенство 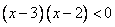
Внесем эти данные в чертеж.

3) 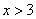 . На этом интервале ситуация не изменяется, значит, для того, чтобы определить ситуацию. Можно взять любое значение из этого интервала и подставить его в произведение.
. На этом интервале ситуация не изменяется, значит, для того, чтобы определить ситуацию. Можно взять любое значение из этого интервала и подставить его в произведение.
Например: 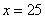
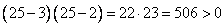
Вывод: при 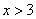 верно неравенство
верно неравенство 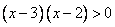
Внесем эти данные в чертеж.

4) Исходное неравенство: 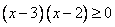 . Уже определено решение строго неравенства
. Уже определено решение строго неравенства 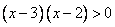 :
:
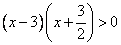 .
.
Равенство нулю: 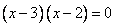 — при
— при 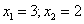 . Точки, удовлетворяющие неравенству обозначаются закрашенными, а неудовлетворяющие – незакрашенными.
. Точки, удовлетворяющие неравенству обозначаются закрашенными, а неудовлетворяющие – незакрашенными.

Окончательный ответ: 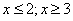
Пример 2: Решить неравенство 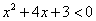 .
.
Краткое оформление решения:
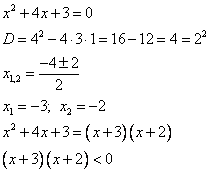
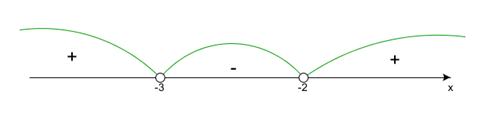
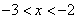
Ответ: 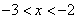 .
.
Более подробно Метод интервалов рассмотрен в соответствующей статье.


