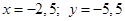Дано: Решить матричным способом систему
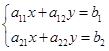
относительно переменных х и у.
Обозначим матрицы коэффициентов и переменных как:
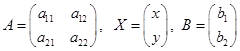
Тогда систему уравнений можно записать как матричное уравнение
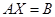 ,
,где требуется найти вектор-столбец Х.
Домножим обе части равенства на
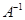 слева.
слева.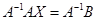
Известно, что
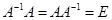 .
.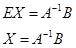
Все, результат произведения
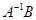 и является ответом.
и является ответом.
Пример 4:
Решить систему уравнений методом обратной матрицы:
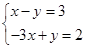 .
.Решение:
Введем обозначения:
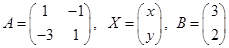
Запишем систему уравнений как матричное уравнение
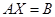 ,
,где требуется найти вектор-столбец Х.
Домножим обе части равенства на
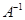 слева.
слева.
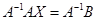
Для того, чтобы вычислить произведение, найдем матрицу, обратную к А. О том, как найти обратную матрицу.
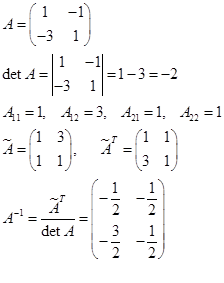
Выполним умножение Операции сложения матриц, умножения матриц, умножения матриц на число.:
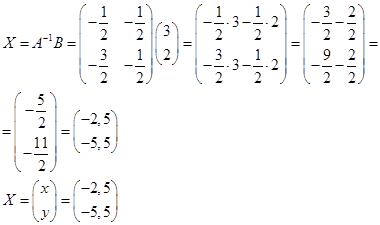
Ответ: