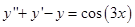Пусть правая часть линейного неоднородного уравнения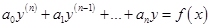 
имеет вид 
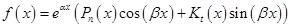, тогда частное решение неоднородного уравнения следует искать в виде: 
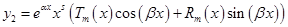, где 
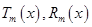— многочлены общего вида степени 
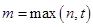, и s равно кратности корня характеристического уравнения 
.
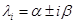Пример 1.
Решить дифференциальное уравнение со специальной правой частью.
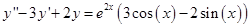
Найдем решение однородного уравнения по корням характеристического.
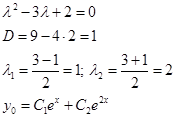
Найдем частное решение неоднородного по виду правой части.
Правая часть имеет вид:
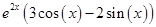
Общий вид:
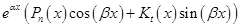
Определим, кто есть кто.
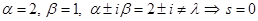
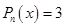— многочлен нулевой степени, значит,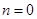 
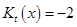— многочлен нулей степени, значит, 
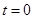, отсюда 
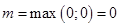, тогда частное решение будем искать в виде: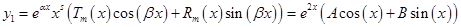
Найдем первые две производные и подставим в исходное уравнение:
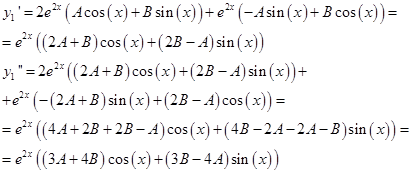
Подставим в исходное:
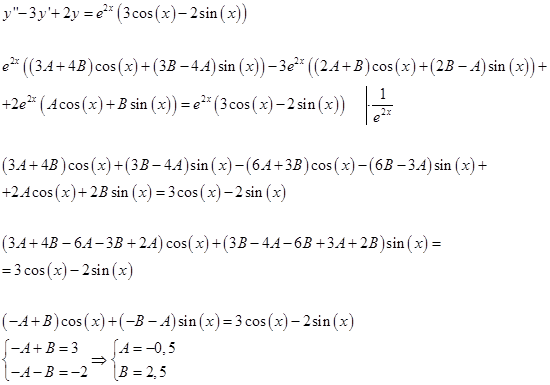
Итого:
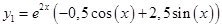
Составим ответ:
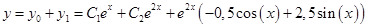
Ответ:
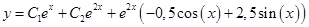
Замечание:
Пусть, например, требуется решить уравнение
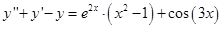, тогда решение будет состоять из трех частей: 
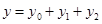, где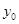
— общее решение однородного уравнения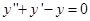 
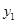— частное решение неоднородного уравнения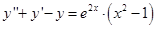 
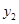— частное решение неоднородного уравнения 