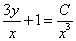Определение: Уравнение вида
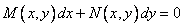, (1)
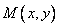где и 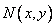— однородные функции одной и той же степени, называется однородным.

Замечание: Функция 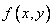называется однородной функцией степени 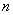, если выполняется равенство .
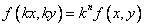Пример 1.
Задание: Выяснить, является ли функция 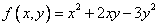однородной.
Решение:


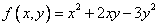
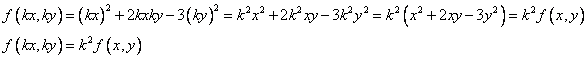
Ответ: Эта функция является однородной функцией степени 2.

Пример 2.
Задание: Выяснить, является ли функция 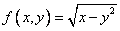однородной.
Решение:

Ответ: Эта функция не является однородной, т.к равенство 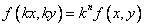не верно ни при каких .
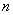Пример 3.
Задание: Выяснить, является ли функция 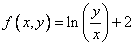однородной.
Решение:

Ответ: Эта функция является однородной функцией степени 0.

Замечание: Общий вид (1) может быть преобразован к виду
.

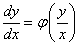Метод решения: Для решения однородного уравнения необходимо сделать замену
,
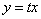где 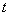— новая искомая функция.
При этом 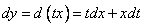, а .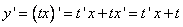
Пример 4:
Решить уравнение .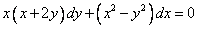
Решение:
Проверим, является ли это уравнение однородным.

Функци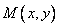и и 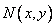являются однородными функциями степени 2. Значит, это однородное уравнение.

Сделаем замену 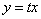и, соответственно, .

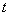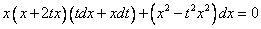
Вынесем за скобки .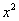
Замечание: При решении однородных уравнений всегда выносится за скобку 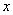в степени, равной степени однородных функций в уравнении.

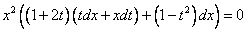
Раскроем скобки и приведем подобные.

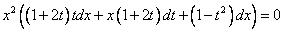
1)
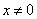
Поделим обе части уравнения на .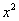

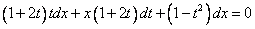
Группируем относительно дифференциалов.

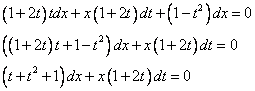
Получили уравнение с разделяющимися переменными. Разделим их.

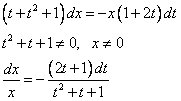
Проинтегрируем обе части уравнения.

Сделаем обратную замену: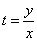

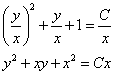
Итог случая : .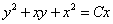
2)
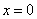
Проверим, является ли 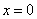корнем уравнения. Подставим его в исходное.

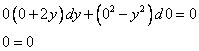
Верное равенство. Значит , 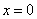является корнем.
Ответ: , .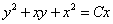
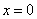Замечание: На 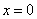в однородных уравнениях всегда нужно обращать отдельное пристальное внимание.

Пример 5.
Решить дифференциальное уравнение
.
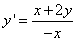Решение:
Проверим, является ли это уравнение однородным.

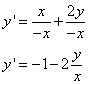
Уравнение приведено к виду 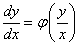, т.е. это однородное уравнение.
Сделаем замену 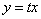и, соответственно, .

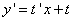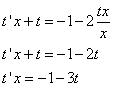
Получили уравнение с разделяющимися переменными. Разделим их.

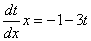
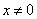, т.к. в исходном уравнении 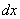стоит в знаменателе, т.е. 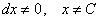, в том числе .
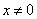1)


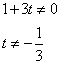
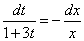
Проинтегрируем обе части уравнения.

Сделаем обратную замену: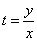

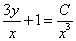
2)
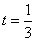
Подставим это значение в уравнение .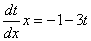
Получили верное тождество. значит, 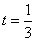является решением дифференциального уравнения. Однако. не стоит выделять это случай в отдельное производство, т.к. он получается в решени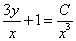и при .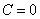
Ответ: