Что такое экстремум понятно, это собирательный термин для минимума и максимума, а условным он называется тогда, когда переменные связаны некоторым условием, дополнительным уравнением связи.
Например:
Найти условный экстремум функции 
, причем должно выполняться 
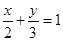( Демидович для ВТУЗов, задача № 2023)
Решение:
Для того, чтобы найти условный экстремум функции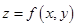 
при условии 
составим функцию Лагранжа вида:
, где 
— неопределенный множитель. После чего ищем обычный экстремум это вспомогательной.
Функция Лагранжа для рассматриваемого предела имеет вид:
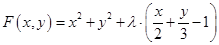
1) Необходимые условия:
Определили точку, подозрительную на экстремум.
2) Достаточные условия.
Для того, чтобы понять, существует ли в этой точке экстремум и какой именно, надо исследовать знак второго дифференциала функции, т.е.
Если он положителен, то это минимум, отрицателен – максимум.
Знак определяется при значениях
, определенных в первом пункте. Причем, 
связанны дифференциалом условия:
Для решаемой задачи:
Здесь он положителен, значит, при
функция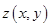 
имеет минимум 
. Это был ответ.Замечание: В этом примере второй дифференциал явно положителен, мы даже не использовали дифференциал условия. Предположим, что мы получили ( при той же критической точке и условии
( Выражение взято с потолка)Здесь, согласитесь, не очевиден знак второго дифференциала, поэтому будем использовать условие:
Подставим во второй дифференциал:
И знак становится очевиден.