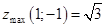Оглавление.
1. Экстремум функции двух переменных.
2. Локальный экстремум функции двух переменных.
3. Случай функции нескольких переменных (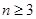
).
Задача: Исследовать на экстремум функцию двух переменных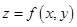 
.
Необходимое условие экстремума.
Как и в случае с функцией одной переменной, где необходимым условием экстремума функции является равенство нулю первой производной. Соответственно, в случае функции нескольких переменных, требуется равенство нулю частных производных по обеим переменных.
Точка
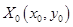, являющаяся решением системы: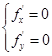
называется стационарной точкой функции
.
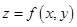Стационарные точки — это точки, подозрительные на экстремум.
Другими словами, в этих точках функция может достигать экстремума, а может и не достигать.
Достаточное условие экстремума.
Для того, чтобы определить, достигает ли функция
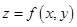экстремума в стационарной точке 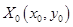введем обозначения: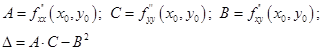
Тогда, если:
•
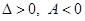— в точке 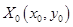функция 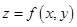имеет максимум.•
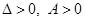— в точке 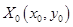функция 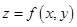имеет минимум.•
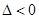— в точке 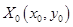функция 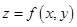не имеет экстремума.•
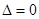— экстремум может быть, а может и не быть, для решения вопроса о существовании экстремума в точке 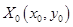требуется применить дополнительные исследования.Пример:
Задача № 2016 из сборника: Задачи и упражнения по математическому анализу для втузов, под ред. Б.П. Демидовича
Исследовать на экстремум следующую функцию двух переменных
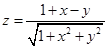
Решение:
Найдем точку, подозрительную на экстремум
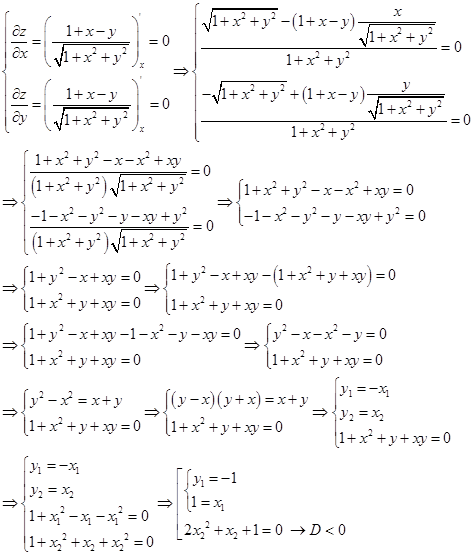
Точка, подозрительная на экстремум
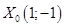
Найдем вторые производные
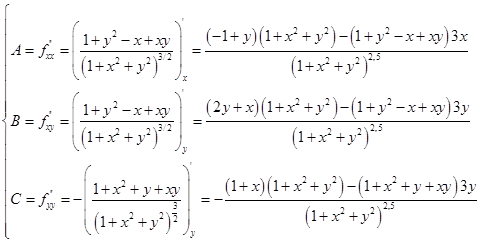
При
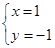
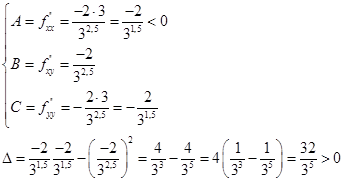
Попался случай
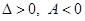— в точке функция 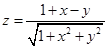имеет максимум.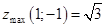
Ответ: