)
Критерий Сильвестра:
Пусть квадратичная форма записана в виде матрицы
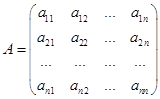
Эта форма является положительно определенной тогда и только тогда, когда все его главные миноры положительны.
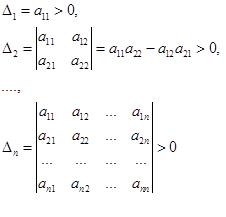
Форма является отрицательно определенной, если ее главные миноры имеют чередующиеся знаки, начиная с отрицательного:
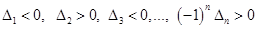.Задача: Исследовать функцию многих переменных
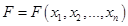на экстремум и вычислить экстремальное значение функции.Решение:
1) Необходимое условие экстремума.
Необходимым условием экстремума функции является равенство нулю первых частных производных (все то же самое, что и для случая двух переменных, только уравнений в системе столько же, сколько переменных в функции).
Точки
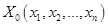, являющиеся решением системы: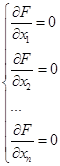
называются стационарными точками функции F.
Достаточное условие экстремума.
Если квадратичная форма
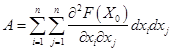,( т.е. квадратичная форма, составленная из вторых производных функции, вычисленных в стационарной точке
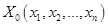) положительно определена, то в этой точке функция имеет минимум, если квадратичная форма отрицательно определена, то максимум. Если квадратичная форма является неопределенной (т.е. принимает и отрицательные и положительные значения при одних значениях переменных), то экстремума в этой точке нет.Для определения знака определенности квадратичной формы удобнее всего применять критерий Сильвестра.
Пример:
Решение задачи № 2018 из сборника: Задачи и упражнения по математическому анализу для втузов, под ред. Б.П. Демидовича
Найти экстремум функции трех переменных
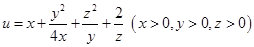.Решение:
1) Необходимое условие экстремума
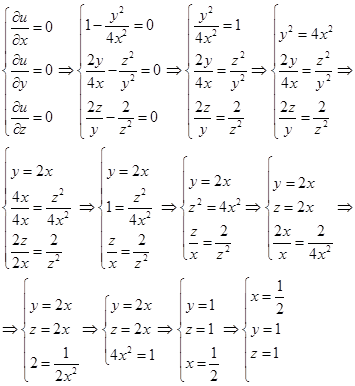
Точка, подозрительная на экстремум:
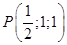
2) Достаточное условие экстремума.
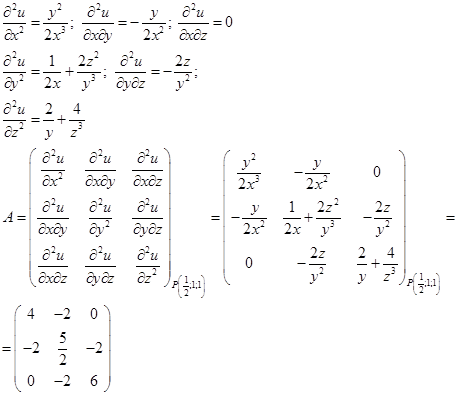
Применим критерий Сильвестра
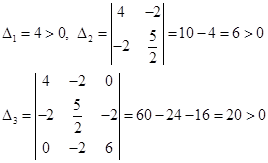
Все миноры положительны, значит, квадратичная форма является положительно определенной и функция имеет в этой точке минимум.
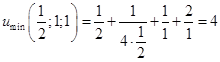
Ответ:
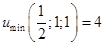
