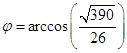Пример 1. (Сборник задач по аналитической геометрии и линейной алгебре, Л.А.Беклемешева, А.Ю.Петрович, И.А.Чубаров., задача №2.1)
Найти скалярное произведение векторов a и b, если:
1) 
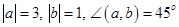
Решение:
Известны длины векторов и угол между ними, т.е. следует использовать формулу
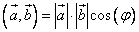.Подставим:
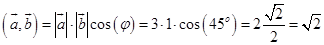
Замечание: угол между векторами острый – скалярное произведение положительно.
Ответ:
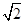
2)
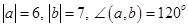
Решение:
Известны длины векторов и угол между ними, т.е. следует использовать формулу
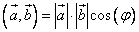.Подставим:
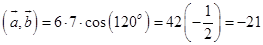
Замечание: угол между векторами тупой – скалярное произведение отрицательно.
Ответ: -21
3)
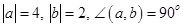
Решение:
Известны длины векторов и угол между ними, т.е. следует использовать формулу
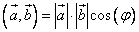.Подставим:
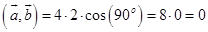
Замечание: угол между векторами прямой (вектора перпендикулярны) – скалярное произведение равно нулю. Этот факт применяют в случае, если требуется определить, являются ли вектора взаимоперпендикулярными.
Ответ: 0
4)
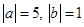, a и b сонаправлены.Решение:
Известны длины векторов и то, что они сонаправлены, т.е. они параллельны или лежат на одной прямой и направлены в одну сторону.
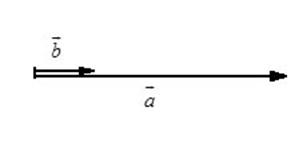
Угол между ними равен нулю. Используем ту же формулу
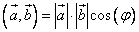.Подставим:
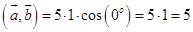
Ответ: 5.
5)
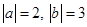, a и b противоположно направлены.Решение:
Известны длины векторов и то, что они противоположно направлены, т.е. они параллельны или лежат на одной прямой и направлены в разные стороны.
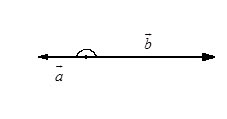
Угол между ними развернутый, т.е. равен 180 градусов.
Подставим:
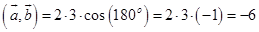
Ответ: -6.
Пример 2.
Найти скалярное произведение векторов
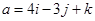и 
.
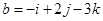Решение:
Здесь векторы a и b заданы как суммы базисных векторов (в ортонормированном базисе), т.е. они имеют координаты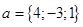 
и 
.
И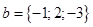звестны их координаты, поэтому для вычисления скалярного произведения применим формулу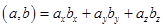 
(стрелочки над векторами ставить не будем, как и в большинстве задачников, но, вообще говоря, они должны быть).
Подставим: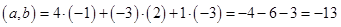 
Ответ: -13.
Пример 3.
Вычислить скалярное произведение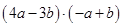 
, если известно, что 
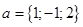и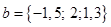 
.
Замечание: здесь использовано альтернативное обозначение операции скалярного умножения векторов: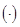 
.
Решение:
Первый вектор в скалярном произведении: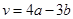 
. Найдем его координаты, используя элементы векторной алгебры.
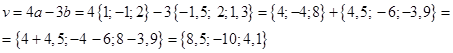
Аналогично со вторым вектором:
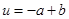. Найдем его координаты, используя элементы векторной алгебры.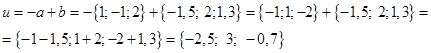
Далее по формуле:
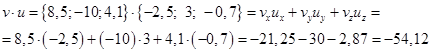
Ответ: -54,12
Пример 4:
Вычислить скалярное произведение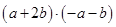 
, если известно, что 
.
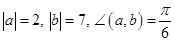Решение:
Здесь неизвестны координаты векторов a и b, поэтому найти координаты векторов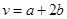 
и 
затруднительно.
Используем свойства скалярного произведения (см. Свойства скалярного произведения векторов.):
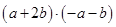=Применим свойство 7)
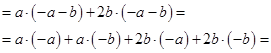
И свойство 6)
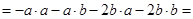
И свойство 3)
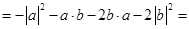
И свойство 1)
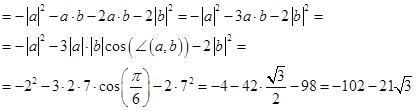
Ответ:
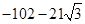
Пример 5.
Найти угол
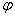между векторам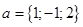и и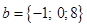 
Решение:
Применим формулу
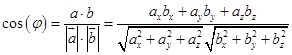
Подставим
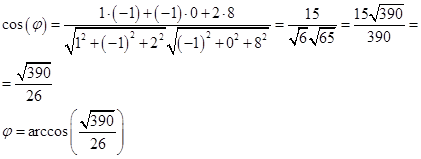
Ответ:
