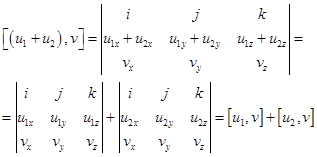1) Векторное произведение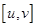 
равно нулю тогда и только тогда, когда векторы коллинеарны.
Пояснение:
Помним, что длина вектора-результата равна произведению длин векторов на синус угла между ними, а т.к. вектора коллинеарны, то угол между ними или ноль или развернутый, а
и 
. Получим: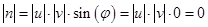
2)
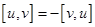(антикоммутативность)Пояснение:
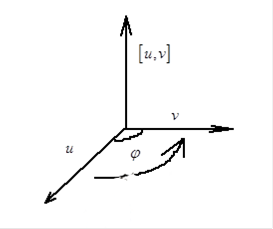и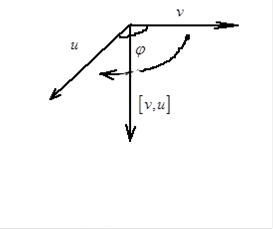 
Из картинок видно, что если поменять порядок векторов, то вектор результат получается по длине такой же, а по направлению противоположный.
3) 
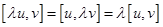, где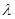 
— произвольное вещественное число.
Пояснение:
Если один из векторов умножить на вещественное число, то его направление останется прежним, а его длина увеличится в 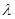раз. Т.е. вектор-результат не изменит своего направления, но его длина увеличится в 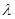раз.
4) 
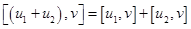или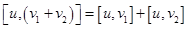 
Пояснение: это свойство векторного произведения легко доказывается из свойств определителей:
