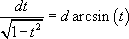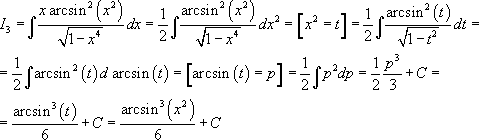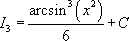1. Вынесение функции из-под знака дифференциала.
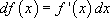
Пример:
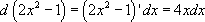
2. Внесение функции под знак дифференциала.
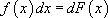 , где
, где 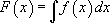 , т.е. является первообразной
, т.е. является первообразной 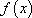 .
.Пример:
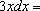
[ Найдем первообразную функции
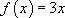
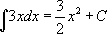 ]
]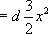
Итог:
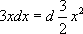
3. Множитель-константу можно выносить за знак дифференциала и вносить под него (частный случай первого и второго правил).
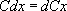
Пример:
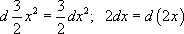 .
.4. Под знаком дифференциала можно прибавлять или отнимать любую константу (частный случай второго правила).
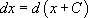
Пример:
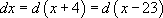
Следующие два правила не относятся к математическим формулам, однако их несоблюдение является одной из самых частых ошибок начинающих.
Одинаковое должно быть одинаковым.
Если в табличной формуле некоторые её части обозначены одинаковыми символами, то и в выражении, к которому будет применена эта формула, соответствующие части должны быть одинаковые.
Пример:
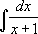
Для нахождения этого интеграла необходимо применить второй табличный интеграл 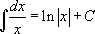 , однако, в его записи знаменатель и переменная интегрирования одинаковы, а в исследуемом интеграле нет. Воспользуемся четвертым правилом, описанным выше: прибавим единицу под знаком дифференциала.
, однако, в его записи знаменатель и переменная интегрирования одинаковы, а в исследуемом интеграле нет. Воспользуемся четвертым правилом, описанным выше: прибавим единицу под знаком дифференциала.
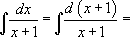
Здесь, для большей наглядности, можно сделать замену 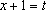
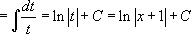 .
.
Правило равновесия.
Если возникает необходимость домножить какую-либо часть выражения на константу, то тут же необходимо выполнить обратное действие, т.е. деление, на ту же константу.
Пример:
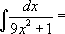
Здесь необходимо воспользоваться третьим табличным интегралом
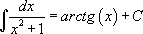 ,
,
но, по предыдущему правилу, в знаменателе первое слагаемое должно быть равно переменной дифференцирования, возведенной в квадрат. Проведем соответствующие преобразования: домножим под знаком дифференциала на 3 и поделим интеграл на 3. Т.к. уже сказано, что множитель-константу можно выносить как за знак дифференциала, так и за знак интеграла, а также можно вносить его обратно, то не принципиально где выполнить обратное действие. В данном случае удобнее уравновешивающий коэффициент  поставить перед интегралом.
поставить перед интегралом.
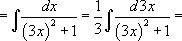
Сделаем замену 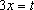 . Воспользуемся табличной формулой, а потом и обратную замену.
. Воспользуемся табличной формулой, а потом и обратную замену.
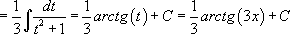 . Это и есть ответ.
. Это и есть ответ.
Примеры применения основных правил интегрирования.
Пример 1. Вычислить интеграл:
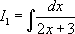
[ Для того, чтобы применить табличный интеграл №2, то есть получить натуральный логарифм, необходимо, чтобы переменная интегрирования и знаменатель были одинаковыми. Воспользуемся третьим правилом: 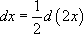 ]
]
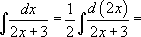
[ Воспользуемся четвертым правилом и прибавим под знаком дифференциала 3 : 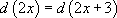 ]
]
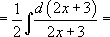 [ Сделаем замену
[ Сделаем замену 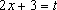 ]
] 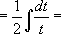 [ Воспользуемся табличным интегралом №2]
[ Воспользуемся табличным интегралом №2] 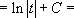 [Сделаем обратную замену]
[Сделаем обратную замену] 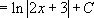
Ответ: 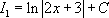 .
.
Пример 2. Вычислить интеграл:
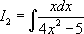
[ На первый взгляд непонятно к какому табличному интегралу стремиться, потому что ни в одной из формул нет ситуации, что в числителе стоит первая степень, а в знаменателе вторая. Применим второе правило: внесем  под знак дифференциала. Найдем для этого первообразную для
под знак дифференциала. Найдем для этого первообразную для  :
: 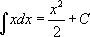 . То есть:
. То есть: 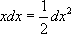 ]
]
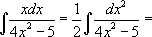
[ По третьему правилу домножим и поделим соответствующие части интеграла на 4]
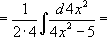 [ по четвертому правилу]
[ по четвертому правилу] 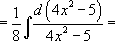
[ сделаем замену 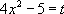 и воспользуемся табличным интегралом №2]
и воспользуемся табличным интегралом №2]
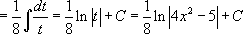
Ответ: 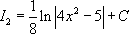
Задачи для самостоятельного решения:
Задание 1. Вычислить неопределенный интеграл:
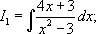
+ Показать/спрятать подсказку №1.
+ Показать/спрятать подсказку №2.
+ Показать/спрятать подсказку №3.
+ Показать/спрятать Решение и Ответ.
Задание 2. Вычислить неопределенный интеграл: 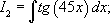
+ Показать/спрятать подсказку №1.
+ Показать/спрятать подсказку №2.
+ Показать/спрятать подсказку №3.
+ Показать/спрятать Решение и Ответ.
Задание 3. Вычислить неопределенный интеграл: 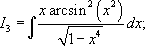
+ Показать/спрятать подсказку №1.
+ Показать/спрятать подсказку №2.
+ Показать/спрятать подсказку №3.
+ Показать/спрятать Решение и Ответ.
Замечание: Вне зависимости от уровня знаний правил и приемов интегрирования настоятельно рекомендуется заучить следующие равенства, чаще всего используемые в тестовых заданиях:
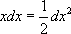 |
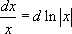 |
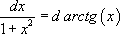 |
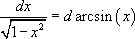
|
Все эти равенства легко доказываются, однако, их необходимо помнить наизусть



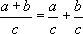
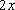 под дифференциал :
под дифференциал : 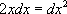 . Во втором применить табличный интеграл №4, где
. Во втором применить табличный интеграл №4, где 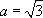 .
.
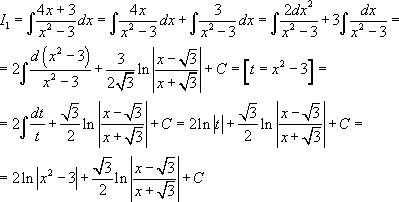
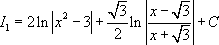
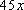 . Для этого в дифференциале домножить на 45, а перед интегралом добавить сомножитель
. Для этого в дифференциале домножить на 45, а перед интегралом добавить сомножитель 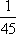 . Сделать замену
. Сделать замену 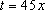 .
.
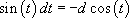 .
.
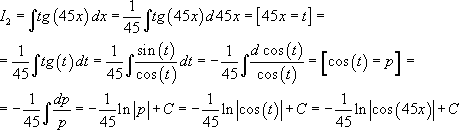
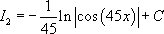 .
.
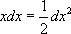
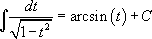 , то, по правилу занесения под знак дифференциала:
, то, по правилу занесения под знак дифференциала: