Оглавление.
1. Первообразная. Таблица интегралов.
2. Основные правила интегрирования.
3. Интегрирование методом подстановки.
4. Тригонометрическая подстановка.
5. Тригонометрическая подстановка 2.
6. Формула интегрирования по частям.
7. Метод неопределенных коэффициентов.
0. Вступление.
Научиться интегрированию не сложно. Для этого необходимо лишь усвоить определенный, достаточно небольшой, набор правил и разработать у себя своего рода чутье. Выучить правила и формулы, конечно же, легко, но понять, где и когда нужно применить то или иное правило интегрирования или дифференцирования, достаточно затруднительно. В этом, собственно, и состоит умение интегрировать.
1. Первообразная. Неопределенный интеграл.
Предполагается, что к моменту чтения этой статьи читатель уже обладает некими навыками дифференцирования (т.е. нахождения производных).
Определение 1.1: Функция 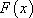 называется первообразной функции
называется первообразной функции 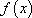 если выполняется равенство:
если выполняется равенство:
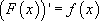
Комментарии:> Ударение в слове “первообразная” можно ставить двумя способами: первообразная или первообразная.
Свойство 1: Если функция 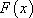 является первообразной функции
является первообразной функции 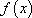 , то функция
, то функция 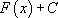 также является первообразной функции
также является первообразной функции 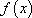 .
.
Доказательство: Докажем это из определения первообразной. Найдем производную функции 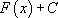 :
:
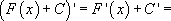
Первое слагаемое по определению 1.1 равно 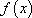 , а второе слагаемое является производной константы, которая равна 0.
, а второе слагаемое является производной константы, которая равна 0.
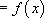
.
Подведем итог. Запишем начало и конец цепочки равенств:
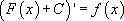
Таким образом, производная функции 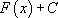 равна
равна 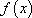 , а значит, по определению, является её первообразной. Свойство доказано.
, а значит, по определению, является её первообразной. Свойство доказано.
Определение 1.2: Неопределенным интегралом функции называется всё множество первообразных этой функции. Это обозначается так:
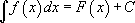
.
Рассмотрим названия каждой части записи подробно:
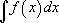 — общее обозначение интеграла,
— общее обозначение интеграла,
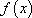 — подинтегральное (подынтегральное) выражение, интегрируемая функция.
— подинтегральное (подынтегральное) выражение, интегрируемая функция.
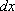 — дифференциал, и выражение после буквы
— дифференциал, и выражение после буквы 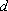 , в данном случае это
, в данном случае это  , будем называть переменной интегрирования.
, будем называть переменной интегрирования.
Комментарии: Ключевые слова в этом определении – “все множество”. Т.е. если в будущем в ответе не будет записано это самое «плюс С», то проверяющий имеет полное право не зачесть это задание, т.к. необходимо найти все множество первообразных, а если С отсутствует, то найдена только одна.
Вывод: Для того, чтобы проверить правильно ли вычислен интеграл, необходимо найти от результата производную. Она должна совпасть с подынтегральным выражением.
Пример:
Задание: Вычислить неопределенный интеграл и выполнить проверку.
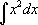
Решение:
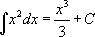
То, как вычислен этот интеграл, в данном случае не имеет никакого значения. Предположим, что это откровение свыше. Наша задача – показать, что откровение нас не обмануло, а сделать это можно с помощью проверки.
Проверка:
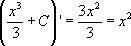
При дифференцировании результата получили подынтегральное выражение, значит, интеграл вычислен верно.
2. Начало. Таблица интегралов.
Для интегрирования не нужно каждый раз вспоминать функцию, производная которой равна данной подынтегральной функции (т.е. использовать непосредственно определение интеграла). В каждом сборнике задач или учебнике по математическому анализу приведена список свойств интегралов и таблица простейших интегралов.
Перечислим свойства.
Свойства:
1. 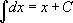
Интеграл от дифференциала равен переменной интегрирования.
2. 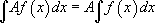 , где
, где 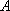 — константа.
— константа.
Множитель-константу можно выносить за знак интеграла.
3. 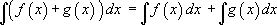
Интеграл суммы равен сумме интегралов (если количество слагаемых конечно).
Таблица интегралов: 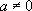
1. 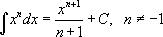 |
10. 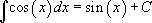 |
2. 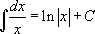 |
11. 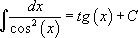 |
3. 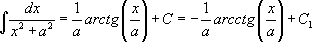 |
12. 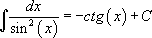 |
4. 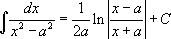 |
13. 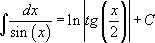 |
5. 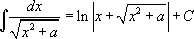 |
14. 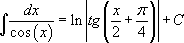 |
6. 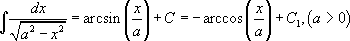 |
15. 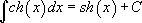 |
7. 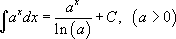 |
16. 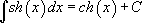 |
8. 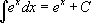 |
17. 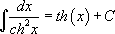 |
9. 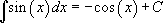 |
18. 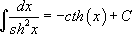 |
Чаще всего задача состоит в том, чтобы с помощью свойств и формул свести исследуемый интеграл к табличному.
Пример:
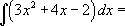
[ Воспользуемся третьим свойством интегралов и запишем в виде суммы трех интегралов.]
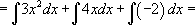
[ Воспользуемся вторым свойством и вынесем константы за знак интегрирования.]
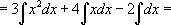
[ В первом интеграле воспользуемся табличным интегралом №1 (n=2), во втором – той же формулой, но n=1, а для третьего интеграла можно или воспользоваться все тем же табличным интегралом, но с n=0, или первым свойством.]
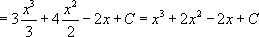 .
.
Проверим дифференцированием:
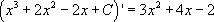
Получено исходное подынтегральное выражение, следовательно, интегрирование выполнено без ошибок (и даже не забыто прибавление произвольной константы С).
Табличные интегралы необходимо выучить наизусть по одной простой причине – дабы знать, к чему стремиться, т.е. знать цель преобразования данного выражения.
Приведем еще несколько примеров:
1) 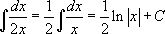
2) 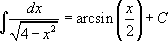
3) 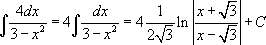
Задачи для самостоятельного решения:
Задание 1. Вычислить неопределенный интеграл:
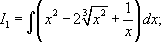
+ Показать/спрятать подсказку №1.
+ Показать/спрятать подсказку №2.
+ Показать/спрятать подсказку №3.
+ Показать/спрятать Решение и Ответ.
Задание 2: Вычислить неопределенный интеграл:
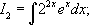 .
.
+ Показать/спрятать подсказку №1.
+ Показать/спрятать подсказку №2.
+ Показать/спрятать подсказку №3.
+ Показать/спрятать Решение и Ответ.
Задание 3: Вычислить неопределенный интеграл:
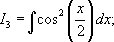
+ Показать/спрятать подсказку №1.
+ Показать/спрятать подсказку №2.
+ Показать/спрятать подсказку №3.
+ Показать/спрятать Решение и Ответ.



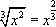
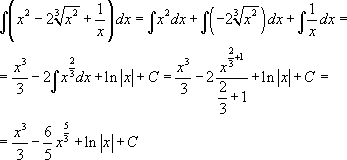
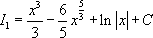
 .
.
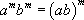 .
.
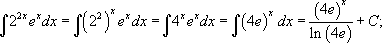 .
.
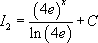 .
.
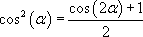 .
.
[…] Самоучитель «Неопределенный интеграл. Основные приемы интегрир… добавлены задачи для самостоятельного решения с […]