Пусть необходимо вычислить неопределенный интеграл 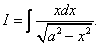. Для определенности будем считать, что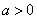
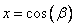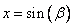В данном случае замена или не даст ничего «выгодного» для дальнейших преобразований, в частности, при такой замене в знаменателе не получиться применить основное тригонометрическое тождество .
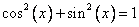Мешает то, что первое слагаемое под корнем не 1.
В таком случае рекомендуется делать замену вида:
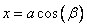или 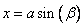(как кому удобно).
Пусть 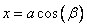и интеграл примет вид

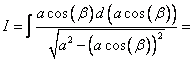
[Проведем преобразования, вынесем функцию из под знака дифференциала и т.д.]

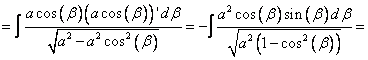
[ По основному тригонометрическому тождеству 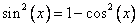. Как и ранее, будем считать, что ]

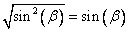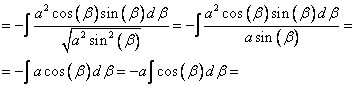
[Интеграл приведен к табличному виду]

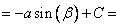
[ обратная замена: ]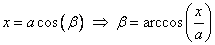
= =

= .
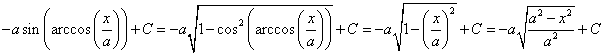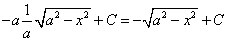Записываем ответ: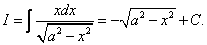
Вывод: Если подинтегральное выражение представляет собой тригонометрическую функцию, то для преобразований его следует помнить две вещи:
1) взаимообратность косинуса и синуса по операции дифференцирования

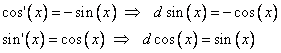
2) Основное тригонометрическое тождество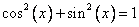

Разобраны еще не все методы работы с тригонометрическими интегралами, основная тригонометрическая замена будет рассмотрена позже.