Для интегрирования некоторых функций применяют формулу:
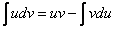.Для правильного применения этой формулы необходимо чётко понимать, что в выражение есть
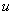, а что есть 
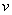, и какая выгода получается от применения этой формулы.Рассмотрим несколько примеров применения этой формулы:
Пример 1.
Вычислить неопределенный интеграл
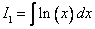
Решение:
Для наглядности можно написать одно над другим:
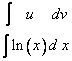
Невооруженным глазом видно, что для применения формулы нужно принять такие обозначения:
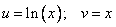.Воспользуемся формулой интегрирования по частям (в записи много пробелов для того, чтобы каждая часть второй строки стояла четко под соответствующей частью первой строки) :
Все. Формулу применили. Дальше используются уже изученные методы интегрирования. В частности, вынесение логарифма из-под знака дифференциала
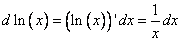
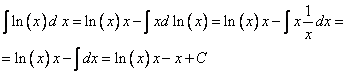
Ответ:
Замечание:
Особо следует обратить внимание на то, что после применения формулы интегрирования по частям та часть, которая стояла «вне» дифференциала (
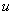) «попадает» под него (
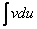), и следующим действием в Примере 1 эта часть выносится из-под знака дифференциала ( 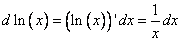) . То есть, от нее находится производная.В предыдущем примере за
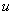был взят 
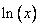и при дифференцирования получили 
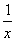, т.е. избавились от логарифма и получили простейший интеграл. Сделаем вывод: за 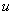лучше всего брать такой сомножитель, производная от которого в данном конкретном случае «выгодна».Применим эти логические выводы к следующему интегралу.
Пример 2.
Вычислить неопределенный интеграл
Решение:
Опять можно использовать запись «одно над другим»:
1) НЕПРАВИЛЬНЫЙ ПУТЬ РАССУЖДЕНИЙ
По аналогии с предыдущим примером можно предположить, что
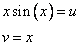
Применим форму интегрирования по частям:
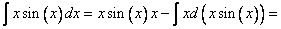
[Вынесем функцию из под знака дифференциала
]
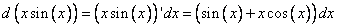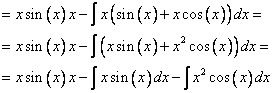
Подынтегральное выражение не только не упростилось, а даже наоборот.
2) Правильный путь рассуждений.
Подынтегральное выражение нужно разделить на 2 части. Это лучше сделать таким образом:
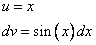
Для применения формулы интегрирования по частям необходимо найти значение .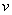
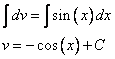
Эта часть решения аналогична занесению под знак дифференциала, при этом тоже находиться первообразная функции.
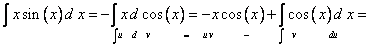
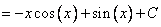
Ответ: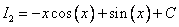 
Пример 3.
Вычислить неопределенный интеграл
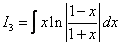
Решение:
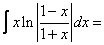
[Очевидно, что хочется избавиться от логарифма, т.е. найти от него производную. Для того, чтобы привести этот интеграл к виду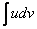 
нужно занести х под знак дифференциала.
]
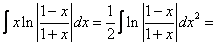
[ Интеграл приведен к виду 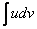, можно применить формулу интегрирования по частям]
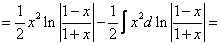
[ выносим функцию из-под знака дифференциала
]
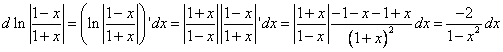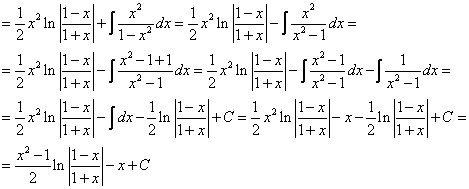
Ответ: 
Бывают также задачи, в которых необходимо применять формулу интегрирования по частям два и более раз.