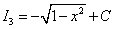В некоторых случаях удобнее от алгебраического подынтегрального выражения перейти к тригонометрическому. Это объясняется удобным свойством функций синус и косинус: производная синуса равна косинусу и, наоборот, производная косинуса равна минус синусу.
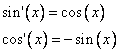
Пример 3.
Вычислить неопределенный интеграл:
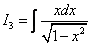
[ Замечание: рассмотрим подынтегральное выражение: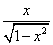 
. Это дробь, а значит знаменатель не должен быть равен нулю. В знаменателе дроби стоит квадратный корень, его подкоренное выражение должно быть неотрицательным.
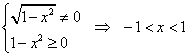
Вывод: подынтегральное выражение определено при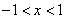 
.
Как известно: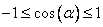 
и 
.
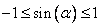Значит, существует такой угол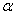 
, для которого будет выполняться равенство :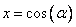 
(или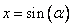 
, это как кому больше нравится).
Все эти слова обязательны потому, что, если ограничения на x например такие: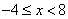 
, то сделать замену нельзя, т.к. .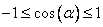
Итак, замена : ]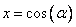
[
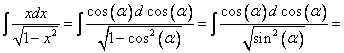
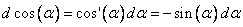
Извлечем корень вот так: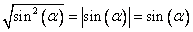 
. Здесь необходимо сделать замечание: если соблюдать все формальности, то нужно записать так:
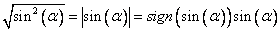, где
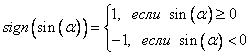
Но, для осознавания процесса замены эти точности не нужны, а при обратной замене неопределенность в выборе знака «+» или «-» опять отпадет.]
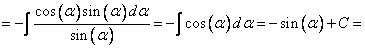
[Сделаем обратную замену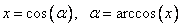 
]
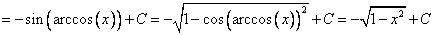
Ответ: