Еще один из немаловажных методов интегрирования – метод подстановки. Говоря проще, необходимо «угадать с заменой» для того, чтобы подынтегральное выражение заметно упростилось, а, в идеале, и свелось к табличному интегрированию. Каких то общих правил для выбора замены не существует, поэтому в этой главе будут показаны наиболее часто встречающиеся, типовые, замены.
Необходимо помнить основное правило при замене: все старые переменные должны «уйти». Другими словами, если в интеграле переменная x , а новая переменная —
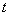 , то после замены в интеграле должна присутствовать только буква
, то после замены в интеграле должна присутствовать только буква 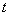 .
.Пример 1:
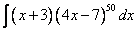
Конечно, можно вычислить этот интеграл непосредственно. Для этого стоит всего-навсего раскрыть 51 скобку, привести подобные слагаемые и т.д. Но это достаточно утомительное занятие.
Сделаем замену:
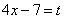
Неопытные и невнимательные люди, прочитав предыдущую строку, запишут следующее выражение:
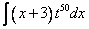 , однако, это НЕПРАВИЛЬНО!!!, потому, что если присмотреться, то переменная интегрирования — x, следовательно,
, однако, это НЕПРАВИЛЬНО!!!, потому, что если присмотреться, то переменная интегрирования — x, следовательно, 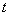 — является константой, а это не так.
— является константой, а это не так.
Сделаем замену ПРАВИЛЬНО:
Требуется вычислить интеграл:
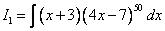
[Сделаем замену: 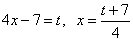 . Здесь выражен непосредственно x через
. Здесь выражен непосредственно x через 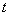 . И везде, где в исходном интеграле стоял необходимо поставить это выражение.]
. И везде, где в исходном интеграле стоял необходимо поставить это выражение.]
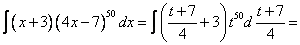
[ В последнем выражении смущает то, что под знаком дифференциала находиться не просто переменная, а функция. Вынесем её из-под знака дифференциала по правилу, описанному выше: 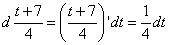 ]
]
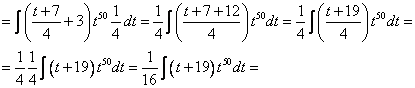
[ В этом подынтегральном выражении раскрыть скобки гораздо проще, чем в исходном]
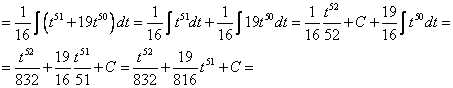
[ Необходимо сделать обратную замену, вернуться к переменной ]
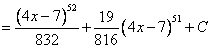
Ответ:
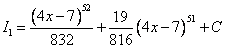
Еще одна частая замена:
Пример 2:
Вычислить неопределенный интеграл:
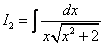
[ Этот интеграл не подходит ни под один из табличных. Сделаем замену, после которой в знаменателе останется только квадратный корень, а первая степень переменной «уйдет».
Замена:
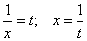 ]
]

[Вынесем функцию из-под знака дифференциала: 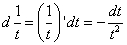 ]
]
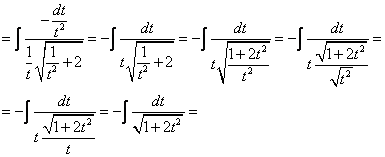
[ Здесь допущена небольшая вольность: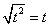 , хотя правильно:
, хотя правильно: 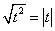 . Но, будем считать, что
. Но, будем считать, что 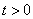 .
.
Выражение приняло более простой вид. Теперь оно практически соответствует табличному интегралу . Мешает только коэффициент при 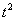 .]
.]
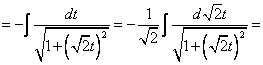
[Вот теперь, когда одинаковые части этого интеграла и табличного стали одинаковыми можно применить формулу]
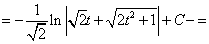
[Обратная замена]
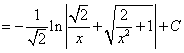
Ответ:
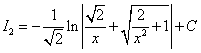
Задачи для самостоятельного решения:
Задание 1. Вычислить неопределенный интеграл: 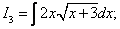
+ Показать/спрятать подсказку №1.
+ Показать/спрятать подсказку №2.
+ Показать/спрятать подсказку №3.
+ Показать/спрятать Решение и Ответ.
Задание 2. Вычислить неопределенный интеграл: 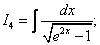
1) Замена: 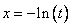
2) 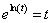
3) 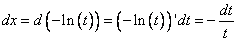
4) Решение:
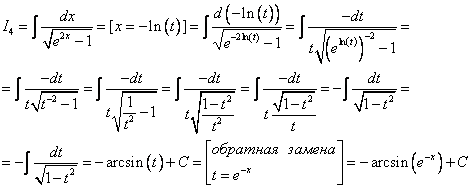
Ответ: 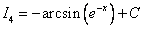



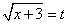
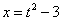
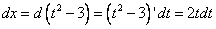
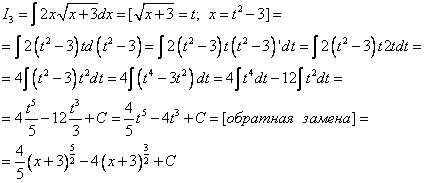
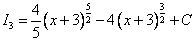
[…] самоучитель по неопределенным интегралам добавлен параграф про интегрирование методом […]