Решение задачи №289 из Сборника задач по линейной алгебре, И.В. Проскуряков.
Задача: вычислить определитель методом выделения линейных множителей
Решение:
Очевидно, что этот определитель представляет собой многочлен степени
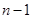, зависящий от переменной х.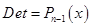
Если
, то второй столбец этого определителя станет кратен первому, а определитель, по свойству, станет равен нулю, т.е.
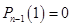
, значит,
является корнем этого многочлена и его можно представить как произведение: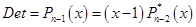
Аналогично и для других столбцов, т.е. 
являются корнями многочлена, значит,
Обратим внимание, что старший член в разложении определителя по степеням х получится при перемножении элементов, стоящих на главной диагонали, если раскрыть все скобки, то получим:
, т.е. коэффициент перед старшей степенью +1, аналогично получится в случае, если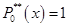 
, т.е. определитель имеет вид:
.