Квадратные уравнения в процессе решения разделяются на три категории.
1) Уравнения, при решении которых получается положительный дискриминант.
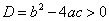
Такие квадратные уравнения имеют два различных действительных корня.
2) Уравнения с дискриминантом, равным нулю.
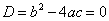
В этом случае высокообразованные школьные учителя говорят, что уравнение имеет один корень, но мы, простые люди, знающие следствие из основной теоремы алгебры, говорим, что это уравнение имеет два корня, просто они одинаковые. Иначе говоря, уравнение имеет один корень кратности два.
3) Уравнения, в которых дискриминант получается отрицательным.
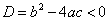
Тут два пути:
а) вы школьник, тогда для вас это уравнение корней не имеет,
б) вы человек, знающий о мнимой единице, тогда это уравнение имеет, опять же, два корня, правда они комплексные.
Рассмотрим примеры на каждый тип.
1. Положительный дискриминант.
Решим квадратное уравнение
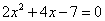
1) Предположим, что мы еще не знаем формул для корней уравнения и будем решать его, выделяя полный квадрат. Преобразования приводятся без комментариев, они аналогичны комментариям с предыдущего параграфа.
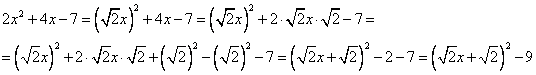
Итак, уравнение примет вид:

Ответ: 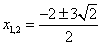
2) Решим это же уравнение с помощью формул для корней.
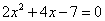
Выпишем значения коэффициентов:
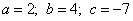
Формулы:
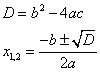
Подставим значения:

Ответ: 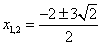
Ответы одинаковые (само собой).
2. Дискриминант равен нулю.
Решим квадратное уравнение
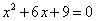
1) Предположим, что мы еще не знаем формул для корней уравнения и будем решать это уравнение внимательно на него посмотрев. А если на него очень внимательно посмотреть, то можно заметить, что этот квадратный трехчлен представляет собой точный квадрат.

Ответ: 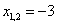
2) Решим это же уравнение с помощью формул для корней.
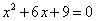
Выпишем значения коэффициентов:
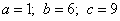
Формулы:
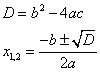
Подставим значения:
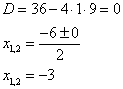
Ответ: 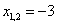
3. Отрицательный дискриминант.
Решим квадратное уравнение
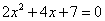
1) Выделяем полный квадрат.
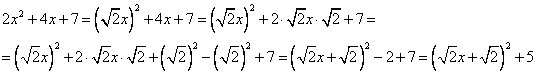
Итак, уравнение примет вид:
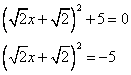
Квадрат выражения равен отрицательному числу.
а) Для школьников.
Если уравнение решается над полем действительных чисел, то корень из отрицательного числа неопределен и это уравнение корней не имеет.
Ответ: корней нет.
б) Если это уравнение решается для комплексных чисел, то, пользуясь определением мнимой единицы:
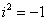
Получаем, что:
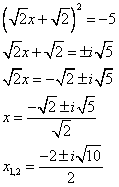
Ответ: 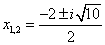
2) Решим это же уравнение с помощью формул для корней.
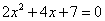
Выпишем значения коэффициентов:
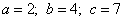
Формулы:
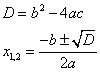
Подставим значения:
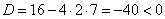
а) Для школьников.
Корень из отрицательного числа неопределен, это уравнение корней не имеет.
Ответ: корней нет.
б) Если это уравнение решается для комплексных чисел, то, пользуясь определением мнимой единицы:
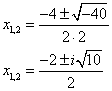
Ответ: 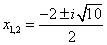
Примеры решений неполных квадратных уравнений в следующем параграфе.


