Оглавление.
1.Выделение полного квадрата. Формулы корней квадратного уравнения.
2.Примеры решения квадратных уравнений.
3.Решение неполных квадратных уравнений.
4.Разложение квадратного трехчлена на сомножители.
Определение:
Уравнение вида
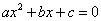, где 
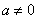
называется квадратным уравнением.
Из любого квадратного трехчлена или многочлена второй степени можно выделить полный квадрат, т.е. преобразовать к виду:
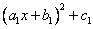.Для того, чтобы выделить полный квадрат необходимо вспомнить формулы сокращенного умножения «квадрат суммы» и «квадрат разности»:
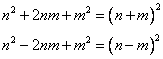
Конечно, следует всегда и везде помнить абсолютно все формулы сокращенного умножения.
Рассмотрим общий вид квадратного трехчлена:
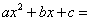
Глядя на формулу «квадрат суммы», нужно привести к такому виду, что первым слагаемым будет квадрат какого-либо выражения:
[
]
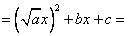
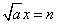Второе слагаемое должно быть в виде удвоенного произведения первого выражения (которое в квадрате) на что-либо еще.
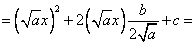
[ Обращаем внимание, что
,
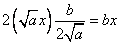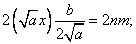т.е.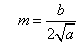 
]
Третье слагаемое должно быть квадратом «остатка» второго слагаемого, его следуем прибавить и, для равновесия, отнять:
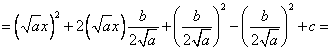
Первые три слагаемые можно свернуть по формуле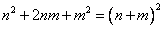 
:
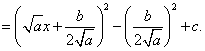
Это и есть полный квадрат (переменная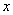 
стоит только внутри скобки)
Формула:
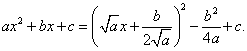
— общий вид выделения полного квадрата из произвольного квадратного трехчлена.
Возвращаемся к решению квадратного уравнения:
Требуется решить квадратное уравнение
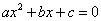
Левую часть можно преобразовать и уравнение примет вид:
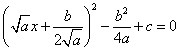
Перенесем вправо второе и третье слагаемые
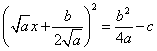
Извлечем корень квадратный из обеих частей равенства. Корень извлекается с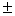 
.
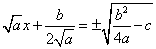
Преобразуем подкоренное выражение:
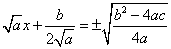
Перенесем второе слагаемое левой части вправо с противоположным знаком:
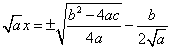
Преобразуем правую часть:
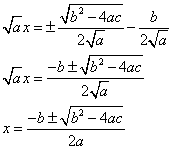
Получены формулы для корней квадратного уравнения. Подкоренное выражение называют дискриминантом и обозначается
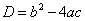.Вывод:
Для решения квадратного уравнения
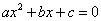
Можно воспользоваться формулами:
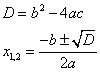
Замечание: Формулы верны также и для неполных квадратных уравнений, т.е. ес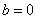ли 
или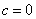 
.
Примеры решения различных квадратных уравнений даны в следующей главе.