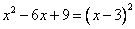До этой поры разговор шел о квадратных уравнениях вида:

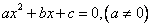
Следует начинать понимать, что объектом исследования является не уравнение, а многочлен.
Определение: Многочленом степени 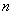переменной называется выражение вида:
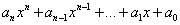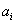, где — числа, вообще говоря, комплексные.
Пример:
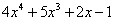— многочлен четвертой степени.
Замечание: Многочлен второй степени часто называют квадратным трехчленом. Даже в случае, если многочлен второй степени имеет вид 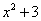. В этом случае слагаемых конечно два, но опытные в математике люди читают его как .
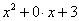Предметом рассмотрения этого параграфа является квадратный трехчлен .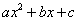

Теоретическая часть:
Теорема:
Для любого многочлена целой степени 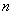справедливо равенство:
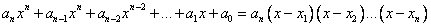, где
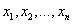— корни многочлена, вообще говоря, комплексные.

Это и есть теорема о разложении многочлена на множители.

Замечание: Корнем многочлена называется такое значение переменной, при подстановке которого в многочлен он обращается в ноль.

Запишем её в применении к квадратному трехчлену:
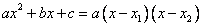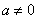где и 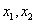— корни квадратного трехчлена, т.е. корни уравнения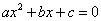

Докажем это, используя формулы для корней квадратного уравнения:

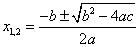
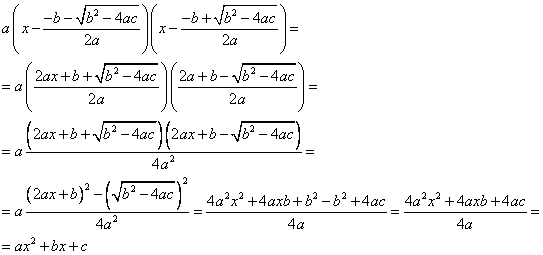
Получили исходное выражение.
Пример 1 (положительный дискриминант):
Разложить на сомножители квадратный трехчлен
.
Решение:
Используем формулу .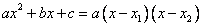
Найдем корни многочлена:

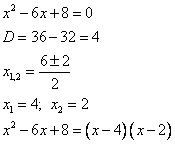
Ответ: .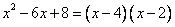
Пример 2 (отрицательный дискриминант):
Разложить на сомножители квадратный трехчлен
.
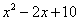Решение:
Используем формулу .
Найдем корни многочлена: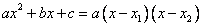

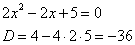
1) Младшим школьникам в этом случае следует говорить, что многочлен на сомножители не раскладывается.
2) Те, кто помнит про комплексные числа, продолжают решение:


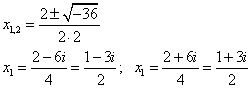
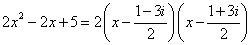
Ответ: .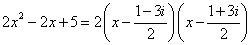

Пример 3 (дискриминант равен нулю):
Разложить на сомножители квадратный трехчлен
.
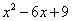Решение:
Используем формулу .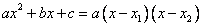
Найдем корни многочлена:

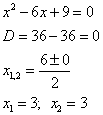
Замечание: Следует помнить, что это уравнение имеет не один корень, а два, но одинаковых. Этот квадратный трехчлен является точным квадратом.

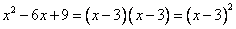
Ответ: