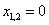Определение: Квадратное уравнение 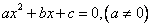называется неполным, если хотя бы один из коэффициентов 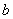и 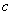равен нулю.

Замечание: Это условие можно записать так: .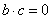
Замечание: Любое квадратное уравнение можно решить по формулам для корней квадратного уравнения. В этом параграфе рассматриваются решения без применения этих формул, вручную так сказать.

1. Коэффициент при первой степени переменной равен нулю ( ).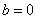

Уравнение принимает вид:

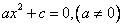
Решим его в общем виде:

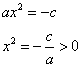
Замечание: уравнение будет иметь корни только в том случае, если 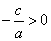, иначе окажется, что квадрат равен отрицательному числу, а это невозможно.

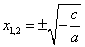
Ответ: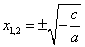
Пример:

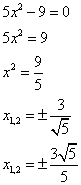
Ответ: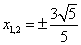
Последний переход сделали потому, что приличные люди иррациональность в знаменателе оставляют крайне редко.

2. Свободный член равен нулю ( ).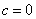

Уравнение принимает вид:

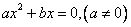
Решим его в общем виде:

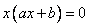
Произведение двух сомножителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю
1)

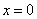
2)

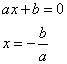
Ответ: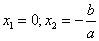
Пример:

Ответ: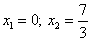

3. Все коэффициенты, кроме стоящего при квадрате переменной, равны нулю.

Уравнение принимает вид:

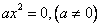
Оно имеет только нулевое решение.
Ответ: