Утверждение:
Натуральное число делится на 5 тогда и только тогда, когда оно оканчивается на 0 или 5.
Доказательство:
Докажем, что если число заканчивается на 0 или 5, то оно делится на 5.
Дано произвольное натуральное число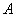 
. Его можно представить в виде суммы:
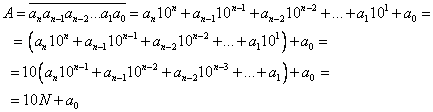.Заметим, что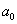 
— количество единиц числа 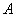, его последняя цифра.
Слагаемое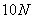 
делится на 5, значит, по Теореме 1, если второе слагаемое, 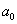, делится на 5, то и вся сумма, т.е. число 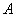делится на 5.
Доказательство обратного утверждения.
Докажем, что если число делится на 5, то оно оканчивается на 0 или 5.
Возьмем представление числа 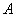, полученное выше:
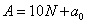, и перегруппируем слагаемые:
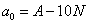. По условию 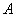делится на 5, т.е. его можно представить в виде: 
.
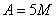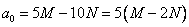
, т.е. число делится на 5. Известно, что
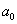— количество единиц исходного числа, т.е. однозначное число, а из однозначных чисел на 5 делится только 5 и 0.
Пример: число 546890 делится на 5, потому, что оканчивается на 0. Число 789451 не делится на 5, т.к. оканчивается на 1, т.е. не на 5 и не на 0.