Оглавление.
1. Основные определения и теоремы.
2. Признак делимости на 2.
3. Признак делимости на 3.
4. Признак делимости на 4.
5. Признак делимости на 5.
Основные определения и теоремы.
Предмет изучения этой статьи – целые числа.
Такие арифметические операции, как сложение, вычитание и умножение целых чисел в результате дают так же целое число. Особое внимание следует обратить на деление двух целых чисел, т.к. результатом такого деления может быть и не целое число.
Определение: Натуральными называются целые неотрицательные числа такие, как 0,1,2…
Замечание: В пределах этой статьи под «числом» следует понимать «целое число».
Определение: Число a делится на число b (или, что то же самое, число b делит число a), если существует такое число c, что верно равенство
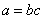 .
.Запись факта делимости числа a на число b :
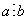 .
.Этот знак, три точки, обозначает лишь то, что число делится на другое число, и совсем не проводит какое либо действие с этими числами, как например, знак +, который производит сложение двух чисел и выдает результат этого действия.
Всегда, когда при прочтении текста встречается запись 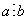 , следует читать «число а делится на число b«.
, следует читать «число а делится на число b«.
Важное замечание: В формулировке некоторых теорем, утверждений и т.п. часто встречается фраза «…тогда и только тогда, когда…».
Например: «Свойство a выполняется тогда и только тогда, когда выполняется свойство b.»
Эту длинную разу можно разбить на две:
1) «Свойство a выполняется тогда, когда выполняется свойство b.»
2) «Свойство a выполняется только тогда, когда выполняется свойство b.»
Первое обозначает, что если есть b, то из него следует a, а второе обозначает обратное, что если есть a, то есть и b. При доказательстве теорем и утверждений для этих случаев используется терминология «туда» и «обратно». Фраза «необходимо и достаточно» имеет абсолютно аналогичное значение.
Встречается обозначение: 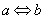 , т.е. туда:
, т.е. туда: 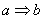 и обратно:
и обратно: 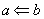 .
.
Замечание: При доказательстве теорем на делимость требуется посимвольное представление многозначного числа. Например, число 543. У него количество единиц – 3 шт., количество десятков – 4 шт., и 5 сотен, т.е. 5,4 и 3 – это цифры, то есть символы, и из них уже составляется число 543.
Теперь перейдем к переменным. Пусть 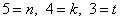 . Как же записать число 543? Если записать
. Как же записать число 543? Если записать 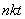 , то возникает проблемка – в математике зачастую не пишется знак умножения, и в этом случае получится, что
, то возникает проблемка – в математике зачастую не пишется знак умножения, и в этом случае получится, что 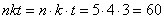 , а совсем не 543.
, а совсем не 543.
В случае, если требуется именно символьная запись, над числом ставят черту: 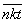 . Она и говорит, что эти буквы надо воспринимать именно как символы.
. Она и говорит, что эти буквы надо воспринимать именно как символы.
Пример: Число 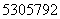 можно представить несколькими способами:
можно представить несколькими способами:
1) Если 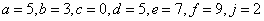 , то
, то
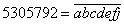 .
.2) Если
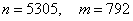 , то
, то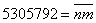 .
.3) Если
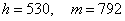 , то
, то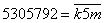 .
.Простейшие свойства делимости:
1) 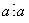 (рефлексивность делимости).
(рефлексивность делимости).
2) Если 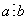 и
и 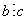 , то
, то 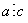 (транзитивность).
(транзитивность).
3) Если 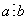 и
и 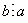 , то либо
, то либо 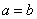 , либо
, либо 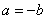 (антисимметричность).
(антисимметричность).
4) Если 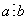 и
и 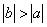 , то
, то
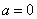 .
.
5) Для того, чтобы 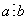 необходимо и достаточно, чтобы
необходимо и достаточно, чтобы 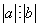 .
.
6) Если 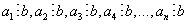 , то
, то
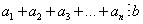 .
.Но, если не вдаваться в тонкости, то для доказательств признаков делимости будут использоваться две теоремы:
Теорема 1:
Пусть 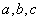 — натуральные числа. Если
— натуральные числа. Если 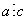 и
и 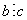 , то
, то 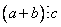 .
.
(Если каждое из слагаемых делится на какое-либо число, то и все сумма делится на это число.)
Доказательство:
Если 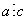 и
и 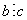 , то, по определению делимости, существуют такие числа
, то, по определению делимости, существуют такие числа 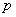 и
и 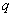 , что верны равенства:
, что верны равенства:
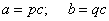 .
.Складываем равенства (левую часть первого равенства складываем с левой частью второго, а правую – с правой):
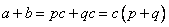 .
.Получили, что существует такое число
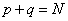 , что верно равенство
, что верно равенство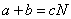 .
.Это и означает по определению делимости, что 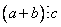 (сумма делится на с ).
(сумма делится на с ).
Теорема доказана.
Теорема 2:
Пусть 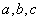 — натуральные числа. Если
— натуральные числа. Если 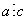 , то и
, то и 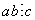 .
.
(Если в произведении хотя бы один сомножитель делится на какое-либо число, то и все произведение делится на это число.)
Доказательство:
Пусть дано произведение 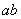 и
и 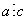 , т.е. a можно представить как
, т.е. a можно представить как 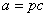 , где p — натуральное число.
, где p — натуральное число.
Исходное произведение получается в виде:
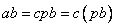 .
.Это, по определению делимости, и обозначает делимость произведения
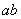 .
.

