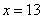Пример 1:
Решить уравнение: 
Решение:
Для того, чтобы решить уравнение
достаточно вспомнить определение логарифма: из равенства
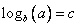следует 
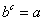.Применим его:
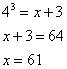
Замечание: единственное ограничение, которое накладывается на значение переменной: аргумент логарифма должен быть больше нуля, т.е.
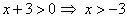. Полученное значение 
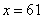подходит.Ответ:
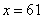
Пример 2:
Решить уравнение: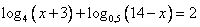 
Решение:
В выражении
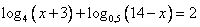
Присутствуют логарифмы с разным основанием: 4 и 0,5. Конечно же стоит попробовать перейти к одному основанию. Например, к 4.
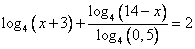
И о чудо! Знаменатель то можно вычислить, т.к.
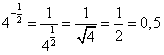
Для коэффициента во втором слагаемом следует применить свойство «Логарифм степени»
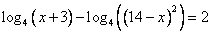
А теперь следует применить свойство логарифмов «Логарифм частного».
И определение логарифма:
Дробь равна нулю тогда и только тогда, когда числитель равен нулю, а знаменатель не равен нулю, т.е
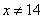и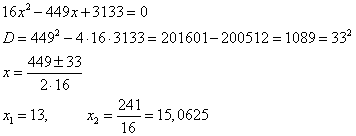
Эти корни не равны 14. Осталось определиться с ограничениями функции логарифм.
Обратимся к исходному уравнению:
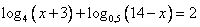
Логарифмируемые выражения должны быть положительны
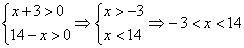
Т.е. ОДЗ для этого уравнения:
.
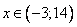В этот интервал попадает только значение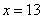 
.
Ответ: