Определение: Функция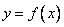 
называется возрастающей , если из неравенства
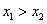
следует неравенство
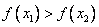
Другими словами: большему значению аргумента соответствует большее значение функции.
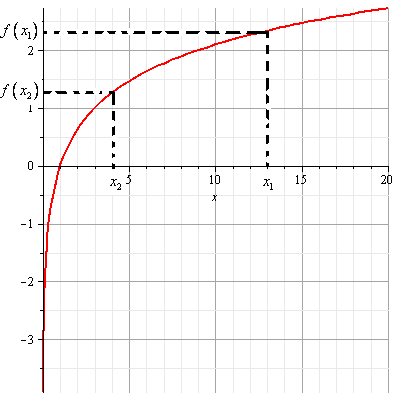
Пример:
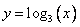
Определение: Функция
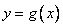называется убывающей, если из неравенства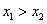 следует неравенство
Другими словами: большему значению аргумента соответствует меньшее значение функции.
Пример:
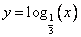
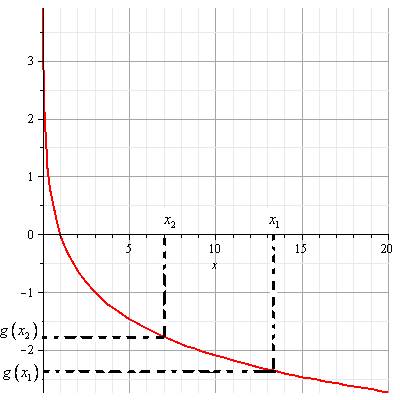
Замечание: Особенностью решения логарифмических уравнений является то, что функция логарифма может быть как убывающей, если основание от 0 до 1, так и возрастающей, если основание больше 1.
Пример 1:
Решить неравенство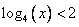 
.
Решение:
Замечание: При решении уравнения вида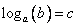 
нужно всего-навсего использовать основное логарифмическое тождество и получить алгебраическое уравнение: 
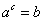. При решении логарифмических неравенств вида 
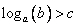так поступить нельзя, потому что это неравенство, т.е. нельзя применить тождество.
Итак, дано неравенство
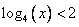
В левой части стоит логарифм по основанию 4.
В правой части стоит число 2. Запишем его в виде логарифма по основанию 4:
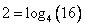
Уравнение примет вид:
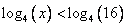
И тут начинается самое интересное. В левой и правой части стоят логарифмы по основанию 4, т.е. сравниваются два значения функции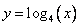 
. Построим схематический график этой функции. Основание логарифма больше 1, значит это возрастающая функция.
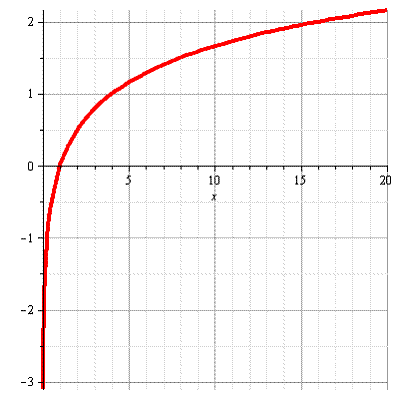
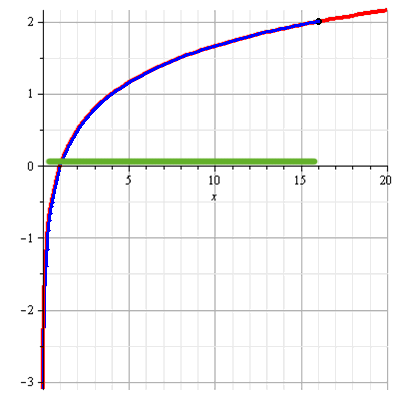
Отметим точку с координатами (16;2) и покажем тот кусок графика, для которого верно неравенство
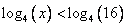(синий цвет). Значения аргумента, при которых это неравенство верно обозначено зеленым цветом.
Далее говорим: Функция
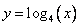— возрастающая, т.е. большему значению аргумента соответствует большее значение функции.Простыми словами: отбрасываем знаки логарифмов и не меняем знак.
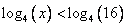
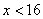
Определим ОДЗ для этого неравенства. Единственное ограничение, накладываемое на переменную – аргумент логарифма должен быть больше нуля, т.е.
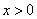.Накладываем это ограничение на полученное неравенство и получаем ответ:
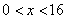
Ответ:
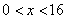
Пример 2:
Решить неравенство:
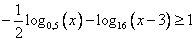
Решение:
Найдем ОДЗ переменной для этого неравенства из соображения, что аргумент логарифма должен быть положительным.
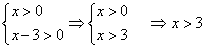
Итого, ОДЗ:
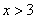, в интервальной записи это выглядит так: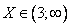 
Приступим непосредственно к решению неравенства.
Основания логарифмов разные. Прейдем везде к основанию 0,5.
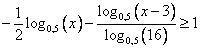
Ну и дальше используем определение и свойства логарифмов:
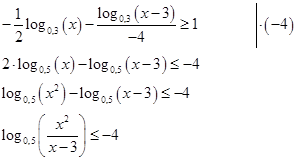
Представим правую часть как логарифм по основанию 0,5
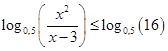
Слева и справа от знака неравенство стоят одинаковые функции
от разных аргументов. Основание этого логарифма равно 0,5, т.е. от 0 до 1, значит это убывающая функция и большему значению аргумента соответствует меньшее значение функции.(отбрасываем log и меняем знак на противоположный):
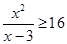
Известно, что
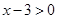(аргумент логарифма может быть только положительный), значит, можно домножить обе части этого неравенства на 
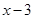и знак неравенства не изменится.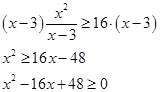
Получили квадратное неравенство. О том, как их решать почитайте в статье: Решение квадратных неравенств.
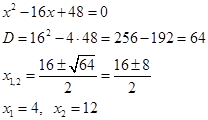
Построим картинку
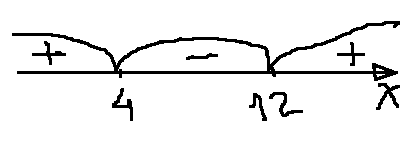
Решается неравенство «
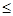», т.е. решение – интервал: 
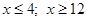.Пересечем с ОДЗ :
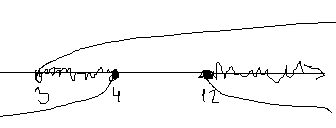
Ответ:
