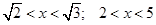Рассмотрим в общем виде:
Здесь засада сразу: в основании логарифма присутствует переменная, и, вообще говоря, нельзя однозначно определить, является ли основание большим 1 или от 0 до 1, т.е. является ли этот логарифм возрастающей функцией или убывающей.
Рассмотрим оба случая.
1)
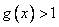, т.е. 
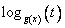— возрастающая функция.Преобразуем неравенство так, чтобы справа была аналогичная функция:
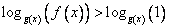.Функция то возрастающая, значит «убираем логарифмы, знак неравенства не меняем».
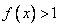
Итог случая: ограничение случая и результат преобразования должны выполняться одновременно, т.е. их можно записать в виде системы неравенств:
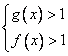
Преобразуем:
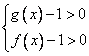
2) 
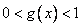, т.е. 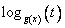— убывающая функция.
.
Функция убывающая, значит «убираем логарифмы, знак неравенства меняем на противоположный».
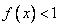
Итог случая: ограничение случая и результат преобразования должны выполняться одновременно, т.е. их можно записать в виде системы неравенств:
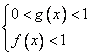
Слукавим, оставив часть
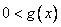для ОДЗ неравенства, как, впрочем, и ограничение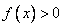 
Получим:
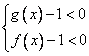
Вывод.
Неравенство свелось к двум случаям:
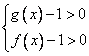или 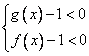.Заметим, что в каждом случае выражения в левых частях одинаковы и сравниваются с нулем.
Помним, что «произведение двух сомножителей больше нуля тогда и только тогда, когда эти сомножители одного знака, или оба положительны, или оба отрицательны».
Так здесь мы это же и видим: или оба положительны, или оба отрицательны. А давайте запишем то, что произведение этих сомножителей должно быть положительным.
Получаем, что системы
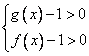или 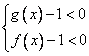равносильны неравенству:
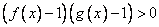.Последний вывод:
Логарифмическое неравенство
равносильно неравенству
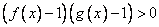.Замечание: не забываем про ОДЗ:
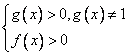
И, соответственно,
Логарифмическое неравенство
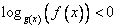
равносильно неравенству
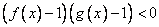.Пример:
Решить неравенство:
Решение:
Начнем с ограничений
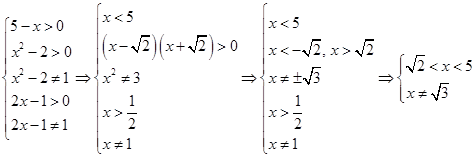
Начнем с общих вещей. Перейдем к одинаковому основанию во всех логарифмах.
Преобразуем:
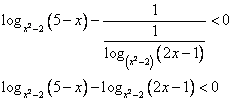
Используем свойство «Логарифм частного»
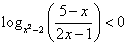
Вот это и есть предмет нашего рассмотрения.
В основании стоит функция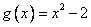 
, в аргументе логарифма стоит функция 
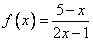и логарифм меньше нуля, значит, он эквивалентен неравенству :
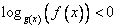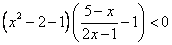
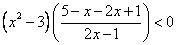
Преобразуем, домножаем на квадрат знаменателя, раскладываем на сомножители первой степени:
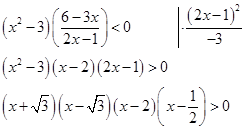
Применим метод интервалов
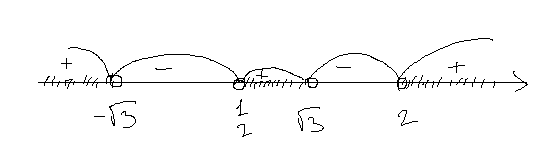
Решение: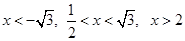 
Пересечем с ОДЗ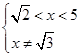 
:
Ответ:
