Оглавление.
1. Определение и график.
2. Свойства логарифмов.
3. Преобразование выражений, содержащих логарифмы.
4. Решение простейших логарифмических уравнений.
5. Решение логарифмических неравенств.
6. Решение логарифмических неравенств с переменной в основании и в аргументе одновременно.
Определение и график функции логарифм.
Определение:
Логарифмом числа а (
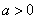) по основанию b (
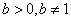) называется такое число с, что верно равенство: 
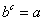. Обозначение: 
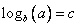.Иначе говоря, логарифм, это степень, в которую надо возвести основание логарифма, чтобы получить аргумент.
Пример:
1) 
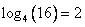, т.к.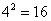 
2) 
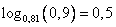, т.к.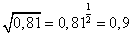 
3) 
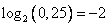, т.к.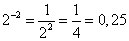 
Замечание: Общепринятые обозначения:
1) 
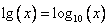— десятичный логарифм.
2) 
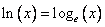— натуральный логарифм
Связь между показательной и логарифмической функцией.
Функции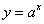 
(показательная) и 
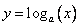(логарифмическая) — взаимообратные, а значит их графики симметричны относительно прямой 
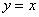(биссектрисы первого и третьего координатных углов).
Пояснение понятия обратная функция:
Рассмотрим логарифмическую функцию
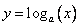,поменяем местами буковки х и у, получим
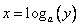.Выразим отсюда у по определению логарифма:
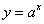.Получили показательную функцию.
Вывод: это взаимно обратные функции.
График.
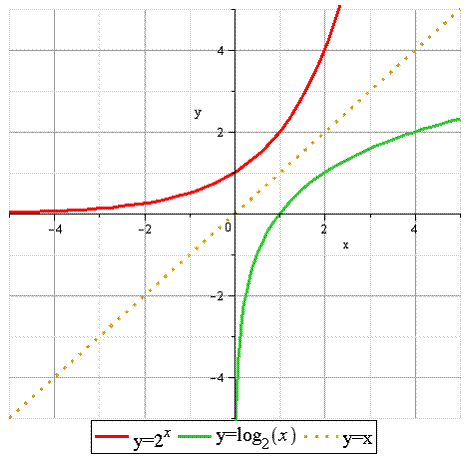
1) Основание логарифма больше 1. (
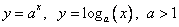)Замечание: Это возрастающие функции, они взаимообратны и их графики симметричны относительно прямой
.
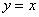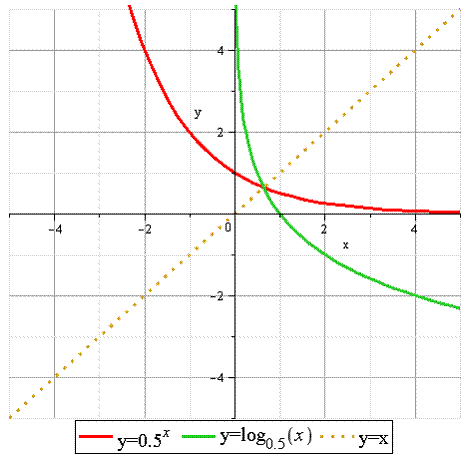
2) Основание логарифма от 0 до 1. (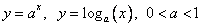
)
Замечание: Это убывающие функции, они взаимообратны и их графики симметричны относительно прямой .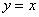
Замечание:
1) Графики функции 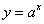всегда проходит через точку с координатами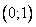 
2) Графики функции 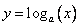всегда проходит через точку с координатами 