Пример 1: Вычислить значение выражения:
Решение:
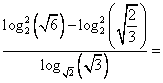
Замечание: При решении задач, содержащих логарифмы, в первую очередь не следует сосредотачиваться на них. Никогда нельзя забывать просто про алгебру.
В числителе этой дроби можно применить формулу сокращенного умножения разность квадратов. Общий вид: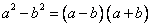 
.
Замечание: В абсолютном большинстве задач следует все логарифмы привести к одному основанию.
В знаменателе воспользуемся формулой перехода к новому основанию и перейдем к основанию 2.
В числителе в первой скобке применим свойство «Логарифм разности», а во второй – «Логарифм суммы».
Самый нижний этаж можно вычислить:
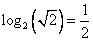
Второй сомножитель в числителе можно вычислить, в знаменателе можно применить свойство «Логарифм степени».
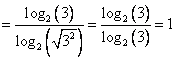
Ответ: 1
Пример 2:
Вычислить значение выражения:
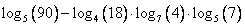
Решение:
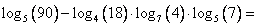
Здесь все просто – перейдем в каждом логарифме к одному основанию. К основанию 5.
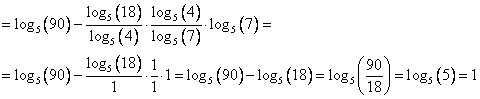
Ответ: 1.
Пример 3:
Вычислить значение выражения:
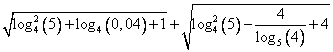
Решение:
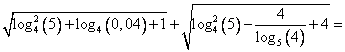
В первом подкоренном выражении все имеющиеся логарифмы имеют одинаковое основание 4.
Однако аргумент второго слагаемого 0,04 очень глаз режет. Следует напомнить, что простые дроби, как правило, предпочтительнее десятичных:
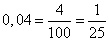
Во втором подкоренном выражении перейдем к основанию 4 во втором слагаемом.
Выражение примет вид:
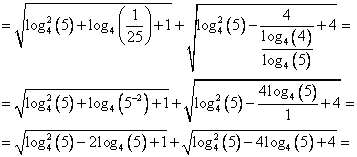
Следует обратить внимание, что подкоренные выражения представляют собой квадратные трехчлены, а если быть точнее, то полные квадраты относительно
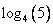.Свернем их:
Помним, что
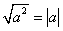
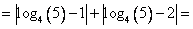
О том, как раскрыть модули можно прочитать в статье ССЫЛКА.
1) Определим, знак первого подмодульного выражения:
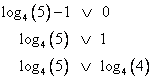
Основание логарифмов равно 4, т.е. больше 1, значит функция
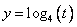— возрастающая и большему значению аргумента соответствует большее значение функции, т.е.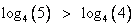
Получили, что:
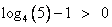и модуль раскрывается: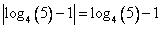 
2) Определим, знак второго подмодульного выражения:
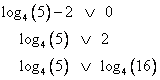
Основание логарифмов равно 4, т.е. больше 1, значит функция
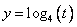— возрастающая и большему значению аргумента соответствует большее значение функции, т.е.
Получили, что:
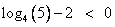и модуль раскрывается: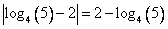
Выражение примет вид:
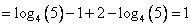
Ответ: 1.