Утверждение: Число делится на 2 тогда и только тогда, когда его оно оканчивается на 2,4,6,8,0, т.е. его последняя цифра делится на 2.
Число, делящееся на 2, называется четным.
Доказательство:
Пусть дано число, оканчивающееся на одну из цифр 2,4,6,8,0. Предположим, без ограничения общности, что оно заканчивается на 4. Его можно записать в виде:
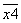(Пример: 3452474, в этом случае 
)и представить в виде суммы:
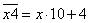(Пример: 
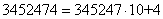)Вынесем за скобку двойку:
(Пример:
)По определению делимости число 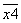делится на 2, т.к. существует число 
, для которого верно равенство
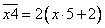, (Пример: 
) .Аналогичные рассуждения можно привести для чисел 2,6,8,0.
Доказательство обратного утверждения:
Пусть дано число A, делящееся на 2, докажем, что оно оканчивается на одну из цифр 2,4,6,8,0.
Представим число A в виде суммы:
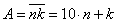.По Теореме, если сумма двух чисел и одно из слагаемых делится на 2 ( число A делится на 2 по условию, первое слагаемое также делится на 2: 
), то и второе слагаемое, слагаемое k делится на 2.
Утверждение доказано.