Давайте рассмотрим, как построить график модуля какой-либо функции не «по точкам», а силой мысли.
Помним, что действие «модуль» из отрицательной величины делает положительную.
Пусть требуется построить график функции
.Построим его перебором случаев в зависимости от знака подмодульного выражения.
1)
Тогда модуль раскроется вот так:
И построим график функции
при этом ограничении 
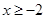
2)
Тогда модуль раскроется вот так:
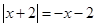
И построим график функции
при этом ограничении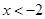 
B функцию запишем в виде:
Итог: Построим график, объединив полученную информацию:
А теперь, давайте построим график похожей функции, например:
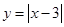, немного подумав.График линейной функции вы можете построить без проблем ( надеемся)
А теперь, вспомним, что модуль отрицательное делает положительным, т.е. ту часть графика, которая лежит ниже оси абсцисс, симметрично «подворачиваем» в верхнюю половину графика. Вот и получим нужный график.
Давайте построим что-то посложнее.
Построим график функции 
Сложно конечно, но мы подойдем последовательно, от простого к сложному. Для начала построим график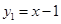 
, потом 
и далее по списку:
Начали:
1)
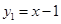
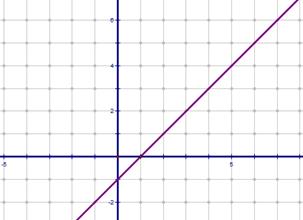
2) , получим этот график, отразив часть, лежащую ниже оси ОХ симметрично нее.
3) 
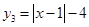, это график получается из предыдущего сдвигом вниз на 4.
4) 
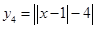, берем последний график и подворачиваем нижнюю часть наверх
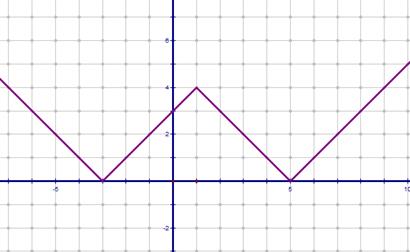
5) И последний шаг 
получим сдвигом на 2 вверх
