Оглавление.
1. Определения и простейшие задачи на вычисление модулей.
2. Уравнения вида  .
.
3. Уравнения вида  (первый способ).
(первый способ).
4. Уравнения вида  (второй способ).
(второй способ).
5. Построение графика модуля функции.
6. Решение уравнений с модулем графическим методом.
7. Решение неравенства с модулем графическим методом.
Определения и простейшие задачи на вычисление модулей.
Одним из простейших типов алгебраических уравнений являются уравнения, содержащие модуль. Дадим определение этого математического объекта.
Определение 1 (основное): Модулем числа 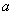 называется величина, вычисляемая по правилу:
называется величина, вычисляемая по правилу:
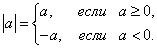
Определение 2: Модулем числа называется абсолютное значение этого числа.
Определение 3 (геометрическое): Модуль числа
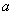 равен расстоянию на числовой прямой от точки с координатой
равен расстоянию на числовой прямой от точки с координатой 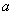 до нуля.
до нуля.Пример:
1) Вычислить
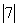 .
.По аналогии с определением, написанным чуть выше,
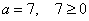 ,
, значит, для того, чтобы раскрыть модуль, нужно пойти по первой строчке определения:
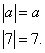
2) Вычислить
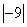 .
.По аналогии с определением:
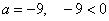 ,
, значит, для того, чтобы раскрыть модуль, нужно пойти по второй строчке определения:
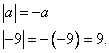
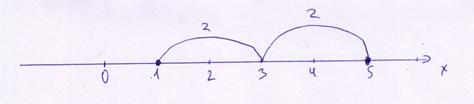
Пример: Отметить на числовой прямой все значение х, такие, что 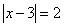 .
.
По геометрическому определению, 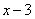 это число, отстоящее от нуля на 2 единицы, т.е.
это число, отстоящее от нуля на 2 единицы, т.е. 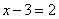 и
и 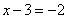 . Получим, что
. Получим, что 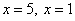 .
.
Замечание:
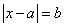 — такие числа, которые от числа
— такие числа, которые от числа 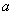 удалены на
удалены на 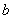 единиц.
единиц.Пример: Отметить на числовой прямой все значение х, такие, что
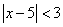 .
.Замечание: По аналогии с предыдущим примером:
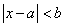 — такие числа, которые от числа
— такие числа, которые от числа 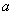 удалены менее, чем на
удалены менее, чем на 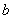 единиц.
единиц.
В этом случае: 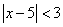 — такие числа, которые от числа 5 удалены менее, чем на 3 единицы.
— такие числа, которые от числа 5 удалены менее, чем на 3 единицы.
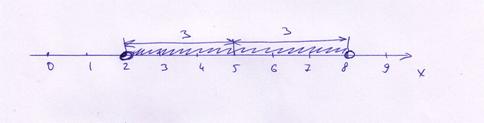
Все эти значения можно записать в виде неравенства:
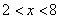
Пример: Отметить на числовой прямой все значение х, такие, что 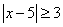 .
.
Замечание: По аналогии с предыдущим примером: 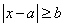 — такие числа, которые от числа
— такие числа, которые от числа 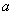 удалены не менее, чем на
удалены не менее, чем на 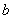 единиц.
единиц.
В этом случае: 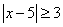 — такие числа, которые от числа 5 удалены не менее, чем на 3 единицы.
— такие числа, которые от числа 5 удалены не менее, чем на 3 единицы.

Все эти значения можно записать в виде объединения неравенств: 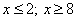
Вывод:
1) Модуль всегда равен положительному числу.
2) Если под знаком модуля положительное число, то знак модуля просто снимается.
3) Если под знаком модуля отрицательное число, то у него меняется знак на противоположный, и оно становится положительным.
Пример:
1) Снять знак модуля: 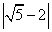
Определим знак подмодульного выражения.
Предположим, что оно положительное:
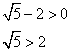
Обе части неравенства одного знака, значит, его можно возвести в квадрат. Они положительны, значит, знак неравенства не изменится.
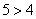
Неравенство верное, значит, и предположение о знаке выражения верное, т.е.
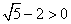 .
.Подмодульное выражение положительно, знак модуля можно просто снять.
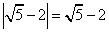 .
.Пример:
Упростить выражение 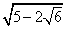 .
.
Здесь нужно помнить две вещи:
а) 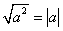 , мы же все-таки про модули тут разговаривает.
, мы же все-таки про модули тут разговаривает.
б) 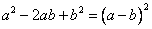 , формула сокращенного умножения квадрат разности.
, формула сокращенного умножения квадрат разности.
Рассмотрим подкоренное выражение и представим его в виде полного квадрата

Замечание:
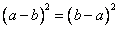 полного квадрата, это просто равенство легко доказывается простым раскрытием скобок.
полного квадрата, это просто равенство легко доказывается простым раскрытием скобок.Замечание: Здесь намеренно выбран порядок слагаемых вида
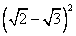 для того, чтобы первый пункт
для того, чтобы первый пункт 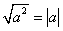 не пропал даром.
не пропал даром.Итак, подставим полученное выражение в исходное
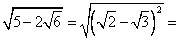
И вот он, первый пункт….
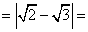
Раскроем модуль по основному определению. Определим знак подмодульного выражения. В этом случае это легко, т.к. интуитивно понятно, что
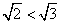 и
и 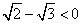 , а, значит,
, а, значит, 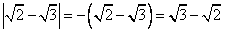 . Вернемся к выражению
. Вернемся к выражению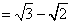
Итог: