Второй способ: В зависимости от значения переменной.
Пример 2:
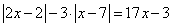
В этом уравнении два подмодульных выражения. Поговорим о них. Первое это 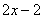 . Это линейный многочлен (многочлен первой степени), он равен нулю при
. Это линейный многочлен (многочлен первой степени), он равен нулю при 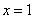 , меньше нуля при
, меньше нуля при 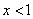 и больше нуля при
и больше нуля при 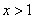 . (эти очевидные факты можно проверить подстановкой соответствующих значений в выражение).
. (эти очевидные факты можно проверить подстановкой соответствующих значений в выражение).
Сделаем вывод, что подмодульное выражение меняет свой знак при переходе переменной через значение 1.
Второе подмодульное выражение 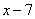 меняет свой знак при
меняет свой знак при 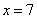 .
.
Ответим на числовой прямой эти точки. Знаки подмодульных выражений изменяются только в этих двух точках, в остальных точках знаки сохраняются. Более подробное объяснение можно прочитать в статье «Метод интервалов для решения квадратных неравенств.»

Разберем все эти случаи. Т.е. все возможные значения переменной х.
1) 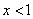 — ограничение случая.
— ограничение случая.

При этих значениях переменной подмодульные значения имеют следующие знаки:
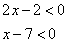
В этом можно убедиться выбрав произвольное значение переменной из ограничения случая и подставив в эти выражения. Пусть 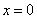
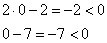 .
.Убедились.
Тогда модули раскрываются вот так:
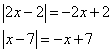
И уравнение принимает вид:
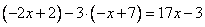
Решим это уравнение
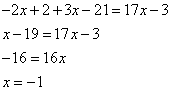

Это значение переменной входит в ограничение случая, т.е.
Ответ случая:
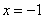 .
.
2 ) 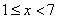 — ограничение случая.
— ограничение случая.

При этих значениях переменной подмодульные значения имеют следующие знаки:
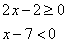
В этом можно убедиться выбрав произвольное значение переменной из ограничения случая и подставив в эти выражения. Пусть
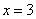
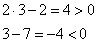 .
.Убедились.
Тогда модули раскрываются вот так:
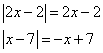
И уравнение принимает вид:
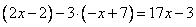
Решим это уравнение
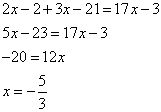

Это значение переменной не входит в ограничение случая, т.е.
Ответ случая: корней нет.
3) 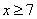 — ограничение случая.
— ограничение случая.

При этих значениях переменной подмодульные значения имеют следующие знаки:
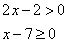
Тогда модули раскрываются вот так:
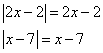
И уравнение принимает вид:
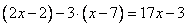
Решим это уравнение
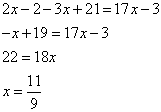

Это значение переменной не входит в ограничение случая, т.е.
Ответ случая: корней нет.
Замечание: все возможные значение переменной х перебрали, теперь надо составить ответ.
Решением задачи является объединение всех ответов, т.е. ответ первого случая.
Ответ: 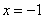


 (второй способ)
(второй способ)