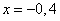Уравнение вида 
Уравнения подобного вида можно решать двумя способами.
Первый способ: В зависимости от знаков подмодульных выражений.
Пример 1:
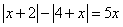
В этом уравнении два модуля, каждое из подмодульных выражений может быть или неотрицательным или отрицательным, т.е. 4 случая:
1) 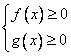 2)
2) 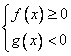 3)
3) 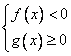 4)
4) 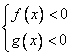
Разберем эти случаи
1)
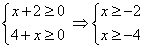

Решение системы: 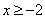 (ограничение этого случая) — при этих значениях переменной оба подмодульных выражения больше или равны нулю, т.е.
(ограничение этого случая) — при этих значениях переменной оба подмодульных выражения больше или равны нулю, т.е.
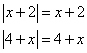
Уравнение примет вид:

Это значение переменной входит в ограничение случая.
Ответ случая: 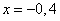
2)
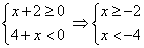

Эта система решений не имеет, т.е. нет таких значений 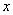 , при которых первое подмодульное выражение было бы неотрицательно, а второе отрицательно, т.е. этот случай в принципе невозможен.
, при которых первое подмодульное выражение было бы неотрицательно, а второе отрицательно, т.е. этот случай в принципе невозможен.
Ответ случая: корней нет.
3)
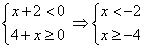
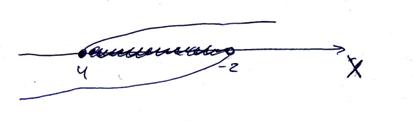
Решение системы: 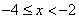 (ограничение этого случая) — при этих значениях переменной первое подмодульное выражение отрицательно, а второе неотрицательно, т.е.
(ограничение этого случая) — при этих значениях переменной первое подмодульное выражение отрицательно, а второе неотрицательно, т.е.
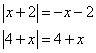
Уравнение примет вид:
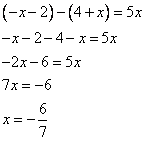
Это значение переменной не входит в ограничение случая.

Ответ случая: корней нет.
4)
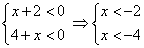

Решение системы: 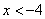 (ограничение этого случая) — при этих значениях переменной оба подмодульных выражения отрицательны, т.е.
(ограничение этого случая) — при этих значениях переменной оба подмодульных выражения отрицательны, т.е.
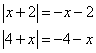
Уравнение примет вид:

Это значение переменной не входит в ограничение случая.

Ответ случая: корней нет.
Для того, чтобы получить решение задачи следует объединить полученные ответы случаев. Ну тут он один, поэтому особых проблем нет.
Ответ: