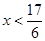Решить неравенство: 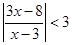
Опять же, будем решать его графическим методом, т.е. построим графики функций
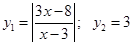
Конечно, график правой части не представляет проблем, давайте разберемся с 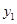 .
.
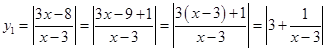
Опять пойдем последовательно:
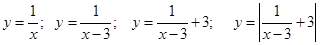
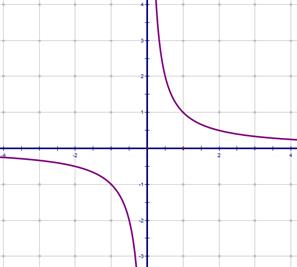
1) 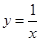 — обычная гипербола.
— обычная гипербола.
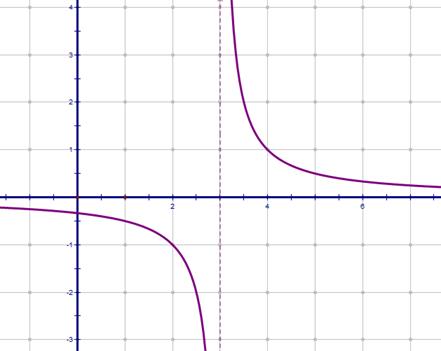
2) 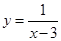 этот график получаем сдвигом предыдущего на 3 единицы вправо.
этот график получаем сдвигом предыдущего на 3 единицы вправо.
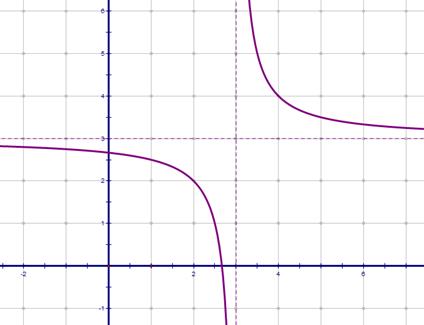
3) 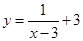 получаем этот график сдвигом предыдущего вверх на 3 единицы.
получаем этот график сдвигом предыдущего вверх на 3 единицы.
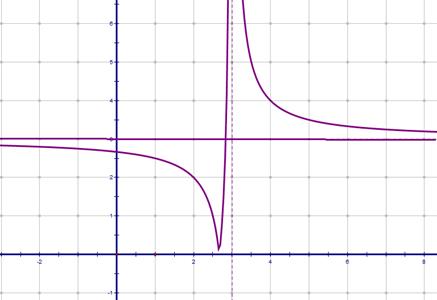
Ну и последний шаг 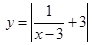 , подвернем отрицательную часть графика
, подвернем отрицательную часть графика
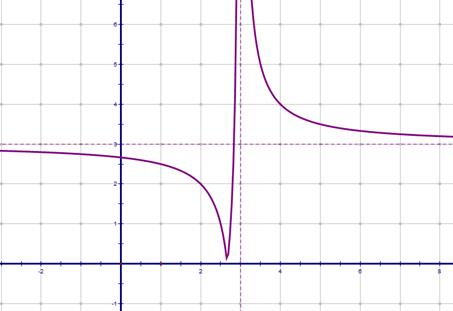
Напоминаем, что вообще-то мы решаем неравенство 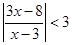 .
.
Проведем прямую 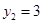 на этом же графике.
на этом же графике.
А теперь осознаем, что нужны значения переменной, при которых
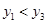 , т.е. график модуля гиперболы лежит НИЖЕ прямой
, т.е. график модуля гиперболы лежит НИЖЕ прямой 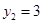 , нам нужны такие ( см. чертеж):
, нам нужны такие ( см. чертеж):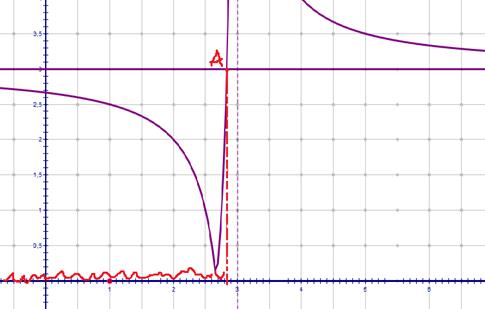
Т.е. нам требуется найти абсциссу точки А, и все х, меньшие нее, будут являться решением неравенства. И тут мы понимаем, что эта точка является пересечением прямой y=3 и той части гиперболы, которую «подгибали», т.е. модуль будет раскрыт с изменением знака и на этом участке функция имеет вид
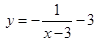 , и уравнение для определения абсциссы будет иметь вид:
, и уравнение для определения абсциссы будет иметь вид: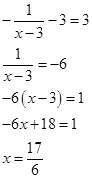
Итог: глядя на чертеж и общую логику задачи, получаем ответ: