Утверждение: Число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3.
Доказательство:
Докажем прямое утверждение.
Рассмотрим любое (натуральное) число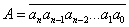 
. Представим его в виде суммы:
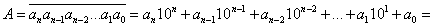
Заметим, что любая степень числа 10 также может быть представленная в виде суммы:
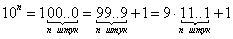
Продолжим операции с числом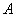 
:
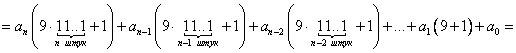
Раскроем скобки и перегруппируем слагаемые
Получили, что число 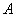можно представить в виде:
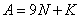,где
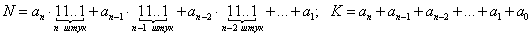,т.е.
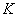и будет равно сумме цифр исходного числа.
Первое слагаемое,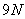 
, очевидно, делится на 3. Если второе слагаемое, 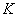, делится на 3, то и все сумма, т.е. число 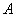будет делиться на 3.
Докажем обратное утверждение.
Число 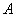делится на 3, значит, сумма его цифр будет делиться на 3.
Выше было показано представление числа 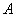в ви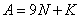де:
, где 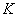— сумма цифр числа 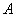. Перенесем слагаемые:
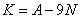.Т.к. по условию 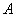делится на 3, то равенство можно записать в виде:
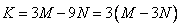.Получили, что 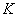делится на 3, т.е. сумма цифр делится на 3.
Утверждение доказано.
Пример: Число 95463 делится на 3 потому, что 9+5+4+6+3=27, а 27 делится на 3.