Утверждение:
Число делится на 4 тогда и только тогда, когда две его последние цифры составляют число, которое делится на 4.
Доказательство:
Пусть дано число 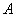 . Воспользуемся методой разложения числа его на сумму, описанной при доказательстве признака делимости на 3:
. Воспользуемся методой разложения числа его на сумму, описанной при доказательстве признака делимости на 3:
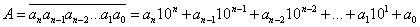 .
.Но сгруппируем слагаемые несколько иначе – отделим последние два слагаемых:
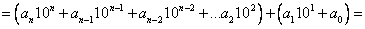
Вынесем из первой скобки 100:
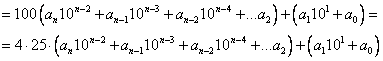
Получилось, что первое слагаемое делится на 4. Значит, и все сумма, т.е. исходное число 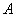 делится на 4 тогда и только тогда, когда второе слагаемое делится на 4.
делится на 4 тогда и только тогда, когда второе слагаемое делится на 4.
Второе слагаемое : 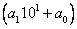 — и есть число, составленное из последних двух цифр исходного числа.
— и есть число, составленное из последних двух цифр исходного числа.
Утверждение доказано.
Замечание: в этом доказательстве нет разделения на доказательство прямого утверждения и обратного, т.к. оно очень простое и содержит в себе всё: если число делится на 4, то число из его последних цифр делится на 4; если последние две цифры числа составляют число, делящееся на 4, то и исходное число делится на 4.
Пример:
Число 24535 не делится на 4, т.к. 35 (число, составленное из последних двух цифр) не делится на 4.
Число 5696 делится на 4, т.к. 96 делится на 4.
Замечание: Доказанный признак делимости на 4 далеко не единственен.
Например:
Двузначное число делится на 4 тогда и только тогда, когда удвоенное количество десятков, сложенное с количеством единиц делится на 4.
Однако, доказанный признак является наиболее часто употребляемым и наиболее удобным.


