Оглавление.
1. Основные понятия.
2. Примеры решений иррациональных уравнений.
3. Частные случаи иррациональных уравнений.
Определение: Иррациональными называются уравнения, в которых переменная стоит под знаком корня или возведена в дробно-рациональную степень.
Пример:
1) 
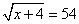
2) 
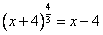
Основные методы и понятия.
При решении иррациональных уравнений следует помнить несколько ограничений:
1) Выражение под корнем четной степени должно быть неотрицательным (т.е.больше или равным нуля).
2) Корень четной степени может принимать только неотрицательные значения.
Пример:
Дано уравнение:
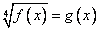
Здесь можно ввести ограничения:
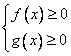
Также следует помнить, что
.
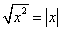Почти каждое уравнение можно решать двумя подходами:
А) найти Область Допустимых Значений (ОДЗ) для переменной и проверить, входят ли в эту область полученные корни,
Б) решать «в лоб», но для всех полученных корней сделать проверку, подставив их в исходное уравнение.
Но лучше перебдеть, чем недобдеть, поэтому в любом случае, всегда-всегда следует стараться сделать проверку. Иногда это затруднительно, особенно если корень получился похожим на нечто такое: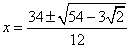 
, но пробовать стоит всегда.
Для того, чтобы показать необходимость проверки полученных корней, рассмотрим два равенства:
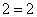и 
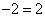
Первое из них верное, а второе – нет.
Возведем обе части каждого из них в квадрат.
Получим
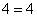и 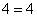Получено два ВЕРНЫХ равенства.
Из этого бесхитростного примера можно сделать вывод: при возведении в квадрат обеих частей уравнения нередко появляются лишние корни, т.к. при возведении в квадрат отрицательные величины становятся положительными.
Решение уравнений вида: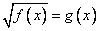 
.
Задача: решить уравнение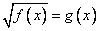
Метод решение:
1) Найдем Область Допустимых Значений переменной, решив систему неравенств
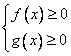
2) Возведем в квадрат обе части уравнения, тем самым избавимся от корня.
3) Решим полученное уравнение
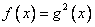
4) Проверим, входят ли полученные корни в Область Допустимых Значений.
5) Сделаем проверку корней, подставив их в исходное уравнение.
Пример 1 (Уравнение имеет корни):
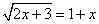
1)
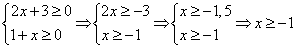
ОДЗ этого уравнения:
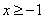
2)
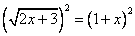
3)
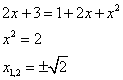
4)
Значение
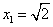является корнем уравнения, т.е. оно входит в ОДЗ, т.к.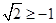 
Значение
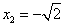не является корнем уравнения, т.к. оно не входит в ОДЗ, т.к.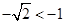 
5) Проверим корень
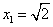, подставим его в исходное равенство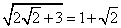
Конечно, можно и в квадрат возвести, но…. вспомним один крайне полезный метод, о котором рассказывается в статье Решение алгебраических уравнений, содержащих модули.
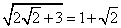
Итак, преобразуем левую часть равенства:
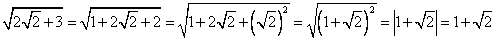
Получили:
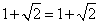равенство верное, т.е. 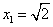является корнем уравнения.
Ответ: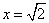 
Пример 2 (уравнение корней не имеет):
Задача: решить уравнение:
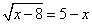
1)
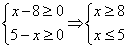
Эта система не имеет решения. Получается, что Область Допустимых Значений не содержит ни одного элемента, т.е. ни одно из значений переменной х не может быть корнем этого уравнения. На этом решение окончено.
ОДЗ этого уравнения:
Ответ: корней нет.
Замечание: Основной метод решения иррациональных уравнений – возведение обеих частей равенства в степень, равную степени корня, дабы от оного избавиться. Но есть еще замены, преобразования, сокращения и т.д. и т.п.