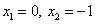Пример 4:
Задача: решить уравнение
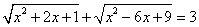
Решение:
Замечание: Возводить в квадрат обе части этого равенства не придется.
Стоит обратить внимание на подкоренные выражения. Под знаком корней стоят квадратные трехчлены:
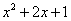 и
и 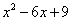 .
. Всегда, когда в уравнении попадаются квадратные трехчлены, следует попробовать или разложить их на сомножители или выделить полный квадрат. Выделение полного квадрата..
Невооруженным глазом видно, что это и есть полные квадраты:
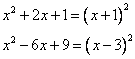
Подставим в уравнение:
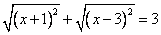
Помним, что
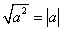
Уравнение примет вид:
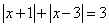
И вот таким нехитрым способом из иррационального уравнения получили уравнение, содержащее модули. А о том, как решать уравнения такого типа можно прочитать в статье Решение алгебраических уравнений, содержащих модули.
Пример 5:
Задача: решить уравнение 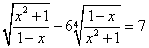
Решение:
Сделаем замену (введение новой переменной), заметим, что в уравнении присутствуют корни степеней 2 и 4. 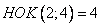
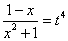
Уравнение примет вид:
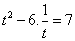
Решим его:
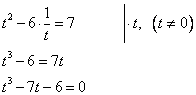
Подберем корень этого уравнения. Если многочлен, в котором коэффициент при старшей степени равен 1, имеет целочисленный корень, то он является делителем свободного члена. В этом многочлене коэффициент при равен 1 и свободный член равен -6, т.е. если это уравнение имеет целочисленный корень, то это или
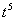 , или
, или 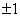 , или
, или 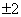 , или
, или 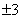 . Проверим
. Проверим 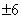 . Подставим в уравнение:
. Подставим в уравнение: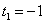
Равенство верное, т.е.
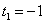 является корнем уравнения, т.е многочлен
является корнем уравнения, т.е многочлен 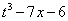 нужно поделить на многочлен
нужно поделить на многочлен 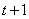 . О том, как это сделать можно прочитать в статье: Деление многочленов уголком..
. О том, как это сделать можно прочитать в статье: Деление многочленов уголком..Получили, что
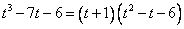 .
.Получили уравнение:
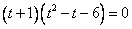
Первый корень известен:
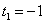
Найдем оставшиеся:
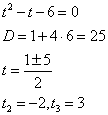
Итого:
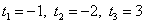
Обратная замена.
1)
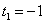

2)
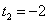
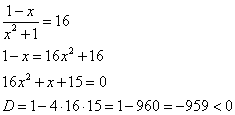
Корней нет.
3)
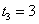
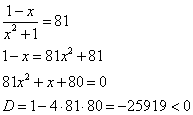
Корней нет.
Проверка покажет, что оба значения 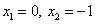
являются корнями этого уравнения.
Ответ: