Список статей:
| 1. Нахождение плотности распределения произведения двух независимых случайных величин. | |
| Описание: | Пример решения задачи на исследование произведения двух независимых величин. |
| 2. Нахождение плотности распределения частного двух независимых случайных величин. | |
| Описание: | Пример решения задачи на составление и исследование плотности распределения частного двух независимых случайных величин. |
| 3. Найти эмпирическую функцию распределения онлайн (on-line). | |
| Описание: | Построение функции распределения эмпирического распределения on-line (он-лайн). |
| 4. Задача 1. | |
| Описание: | По данным, приведенным в таблице: 1) Построить линейное уравнение парной регрессии y на x; 2) Рассчитать линейный коэффициент парной корреляции и оценить тесноту связи; 3) Оценить статистическую значимость параметров регрессии и корреляции, используя F-статистику, t-статистику Стьюдента и путем расчета доверительных интервалов каждого из показателей; 4) Вычислить прогнозное значение y при прогнозном значении x, составляющем 108% от среднего уровня; 5) Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал; 6) Полученные результаты изобразить графически и провести экономическое обоснование. |
| 5. Задача 2. | |
| Описание: | Используя данные, приведенные в таблице: 1) Построить линейное уравнение множественной регрессии; 2) Оценить значимость параметров данного уравнения построить доверительные интервалы для каждого из параметров, оценить значимость уравнения в целом, пояснить экономический смысл полученных результатов; 3) Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной детерминации, сравнить их с линейными коэффициентами парной корреляции, пояснить различия между ними; 4) Вычислить прогнозное значение при уменьшении вектора на от максимального уровня, оценить ошибку прогноза и построить доверительный интервал прогноза. |
| 6. Задача 3. | |
| Описание: | Известны данные о внесении минеральных удобрений под посевы в сель-скохозяйственных организациях. Рассчитать цепные и базисные показатели динамики от года к году и средние показатели динамики за весь период. |
| 7. Задача 4. | |
| Описание: | Имеются некоторые данные о населении Российской Федерации. Учитывая данные о численности населения страны на 1 января каждого года определить: 1. Численность экономически активного населения, численность экономически неактивного населения, коэффициенты экономической активности, занятости и безработицы. 2. Коэффициенты рождаемости, смертности, естественного и миграционного прироста населения, коэффициент Покровского. |
| 8. Задача 5. | |
| Описание: | Известно распределение населения по величине среднедушевых доходов. Определить децильный коэффициент дифференциации доходов. |
| 9. Задача 6. | |
| Описание: | На основе данных определить индексы выработки постоянного, переменного состава и структурных сдвигов. Сделать выводы. |
| 10. Задача 7. | |
| Описание: | На основе данных определить индивидуальные и общие индексы цен, себестоимости, физического объёма реализованной продукции, товарооборота, затрат на производство продукции. Сделать выводы. |
| 11. Задача 8. | |
| Описание: | В ходе анкетирования рассматривалось два признака: потребление продукта А и доход опрошенных. С помощью коэффициентов взаимной сопряженности Пирсона и Чупрова требуется определить, зависит ли частота потребления продукта от дохода опрошенных. |
| 12. Задача 9. | |
| Описание: | По данным определить наличие и направление связи между признаками, построить уравнение регрессии. Построить график теоретического и практического значения Y. |
| 13. Задача 10. | |
| Описание: | Проведено 100 независимых измерений значений непрерывной случайной величины X. Результаты измерений оформлены в виде статистической совокупности. Выполнить статистическую обработку этих данных. Для этого необходимо: 1) записать вариационный ряд (первая строка – варианты, вторая – соответствующие им частоты); 2) записать статистический закон распределения случайной величины X. 3) найти несмещенные оценки математического ожидания и дисперсии случайной величины X. 4) построить гистограмму относительных частот; 5) при уровне значимости 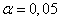 проверить по критерию согласия Пирсона нулевую гипотезу о том, что случайная величина X имеет нормальное распределение; проверить по критерию согласия Пирсона нулевую гипотезу о том, что случайная величина X имеет нормальное распределение;6) если нулевая гипотеза о нормальном распределении случайной величины X принимается, то построить кривую нормального распределения на одном рисунке с гистограммой относительных частот. |
| 14. Задача 11. | |
| Описание: | Пусть над системой двух случайных величин 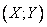 при приодинаковых условиях производится 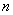 независимых испытаний, и результаты этих испытаний написаны в виде корреляционной таблицы. независимых испытаний, и результаты этих испытаний написаны в виде корреляционной таблицы.Требуется: 1) вычислить условные средние случайной величины Y; 2) найти выборочный коэффициент корреляции; 3) найти выборочное корреляционное отношение Y к X ; 4) в прямоугольной системе координат построить точки 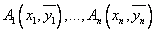 5) записать сумму квадратов отклонений точек, 6) записать систему уравнений для определения неизвестных параметров уравнения регрессии Y на X; 7) найти выборочное уравнение регрессии Y на X ; 8) в прямоугольной системе координат построить кривую регрессии Y на X. |
| 14. Задача 12. | |
| Описание: | По данным, приведенным в таблице: 1) Построить линейное уравнение парной регрессии y на x; 2) Рассчитать линейный коэффициент парной корреляции и оценить тесноту связи; 3) Оценить статистическую значимость параметров регрессии и корелляции, используя F-статистику, t-статистику Стьюдента и путем расчета доверительных интервалов каждого из показателей; 4) Вычислить прогнозное значение y при прогнозном значении x, составляющем 108% от среднего уровня; 5) Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал; 6) Полученные результаты изобразить графически и провести экономическое обоснование. |
| 15. Задача 13. | |
| Описание: | Используя данные, приведенные в таблице: 1) Построить линейное уравнение множественной регрессии; 2) Оценить значимость параметров данного уравнения построить доверительные интервалы для каждого из параметров, оценить значимость уравнения в целом, пояснить экономический смысл полученных результатов; 3) Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной детерминации, сравнить их с линейными коэффициентами парной корреляции, пояснить различия между ними; 4) Вычислить прогнозное значение 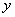 при уменьшении вектора при уменьшении вектора 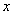 на на 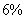 от максимального уровня, оценить ошибку прогноза и построить доверительный интервал прогноза от максимального уровня, оценить ошибку прогноза и построить доверительный интервал прогноза |
| 16. Задача 14. | |
| Описание: | Используя данные, предоставленные в таблице, проверить наличие гетероскедастичности, используя тест Голдфелда-Куандта. |
| 17. Решения нескольких задач по теории вероятностей из сборника Чудесенко. | |
| Описание: | Решения некоторых заданий по теме теория вероятностей и математическая статистика. |
| 18. Решения нескольких задач по теории вероятностей 1. | |
| Описание: | Решения некоторых задач по теории вероятностей. Темы: классическое определение вероятностей, формула полной вероятности, формула Байеса (Бейеса). |
| 19. Решения нескольких задач по теории вероятностей 2. | |
| Описание: | Решения некоторых задач по теории вероятностей. Темы: Функция распределения, плотность распределения, нормальное распределение |
| 20. Решения нескольких задач по теории вероятностей 3. | |
| Описание: | Решения задач по теории вероятностей, темы: неравенство Маркова, биномиальное распределение, распределение Пуассона. |
| 21. Решения задач по математической статистике 1. | |
| Описание: | Математическая статистика, критерий Пирсона, критическая область, доверительный интервал, хи-квадрат |
| 22. Решения задач по математической статистике 2. | |
| Описание: | Решения задач по математической статистике: уравнение регрессии, коэффициент корелляции, групповые средние |
| 23. Критические точки распределения хи-квадрат. | |
| Описание: | Критические точки распределения хи-квадрат. Таблица значений хи-квадрат. Как вычислить хи-квадрат распределение при помощи Excel. |
| 24. Таблица значений функции Лапласа. | |
| Описание: | Таблица значений функции Лапласа, как найти значение функции Лапласа в Excel. |
| 25. Примеры решения различных задач по теории вероятностей. |
| 26. Решение задачи по статистике. | |
| Описание: | Сравнить демографическую ситуацию в Москве и Санкт-Петербурге, рассчитав: 1. Относительные показатели, характеризующие естественное движение населения (коэффициенты рождаемости, смертности, естественного прироста, жизненности Покровского, брачности и разводимости); 2. Показатели структуры численности населения по возрастным группам, а также коэффициенты демографической нагрузки населения (общий, пенсионной нагрузки и нагрузки по замещению). Сформулировать выводы. |
| 27. Доказать тождество c помощью диаграмм Эйлера-Венна и характеристических функций. | |
| Описание: | Пример решения задачи на доказательство тождества двумя методами. |
| 28. Проверка гипотезы о независимости признаков. Пример. | |
| Описание: | Пример решения задачи на проверку гипотезы о зависимости признаков по хи-квадрат критерию. |
| 29. Составить уравнение криволинейной (квадратичной) регрессии. | |
| Описание: | Пример решения задачи на составление уравнения криволинейной (квадратичной) регрессии. |


